
문제설명

입력 & 출력

나의 풀이

이번 문제는 N×M크기의 배열로 표현되는 미로가 있을 때 (1,1)에서 시작해서 주어진 (N, M)까지 가는 최단 거리를 출력하는 문제입니다.
문제를 딱 보면 알 수 있듯이 BFS로 풀어야 합니다. 코드를 나눠서 설명해보겠습니다.

먼저 자주 선언되는 변수들을 전역변수로 선언하여 가독성을 높여줍니다.
N x M의 배열로 표현되는 미로의 크기를 받아줄 N, M 그리고 미로 map, 방문 여부를 체크할 visited를 전역변수로 선언해 줍니다.
그리고 상하좌우로 이동할 dx와 dy를 초기화를 해줍니다. 이 방향 배열은 개인이 어느 방향으로 설정할지에 따라서 다릅니다.
- 상(Up): X 좌표는 위로 이동하므로 dx [] 값이 음수가 됩니다.
- dx [0] = -1, dy [0] = 0
- 하(Down): X 좌표는 아래로 이동하므로 dx [] 값이 양수가 됩니다.
- dx [1] = 1, dy [1] = 0
- 좌(Left): Y 좌표는 왼쪽으로 이동하므로 dy [] 값이 음수가 됩니다.
- dx [2] = 0, dy [2] = -1
- 우(Right): Y 좌표는 오른쪽으로 이동하므로 dy [] 값이 양수가 됩니다.
- dx [3] = 0, dy [3] = 1

main문에서는 먼저 빠른 입력을 위해 BufferedReader클래스를 사용하여 입력을 받아주고, N과 M을 공백으로 분리하여 저장을 해줍니다.
그리고 입력받은 가로 세로 크기만큼 미로와 방문 여부를 체크할 visited배열을 초기화를 해줍니다.
그리고 각 가로에 들어갈 숫자를 받아주고, charAt() 메서드를 사용하여 미로에 저장을 해줍니다. 이때 charAt() 메서드의 반환값은 char타입이기 때문에 '0'나 48을 빼줘야 합니다.
그리고 시작 좌표 (0,0)에서 BFS 알고리즘을 호출하여 (N-1, M-1)까지의 최단 거리를 계산합니다.
BFS(너비 우선 탐색) 알고리즘에서는 각 칸에 대해 현재 위치에서 다음 위치로 이동할 때 거리를 누적하여 계산합니다❗️
문제에서는 (1,1)에서 출발한다고 했지만, (0,0)에서 시작하여 각 칸에 도달할 때마다 거리를 1씩 누적해 주면 되기 때문에 (0,0)으로 시작합니다.

그리고 문제의 핵심이라고 할 수 있는 BFS함수에서는 기본적인 로직은 상하좌우를 이동하면서 방문하지 않았으며, 요소가 1인 즉 이동이 가능한 길을 찾는 것입니다.
BFS는 시작점에서부터 이동 가능한 경로(1)를 찾아가면서 각 칸까지의 최단 거리를 계산하고, 이를 map 배열에 저장합니다.
따라서 BFS를 수행하면서 이동 가능한 칸을 방문하고 그 칸까지의 거리를 이전 칸까지의 거리 + 1로 업데이트하여 저장하는 것이 핵심 로직입니다.
주석을 자세히 달아놔서 특별히 다른 설명은 아니지만 코드를 하나씩 뜯어서 설명하자면 다음과 같습니다.
BFS 동작 방식
- 큐 초기화 및 시작점 설정
- Queue <int []> queue = new LinkedList <>();
- BFS를 위한 큐를 선언하고 초기화합니다.
- queue.offer(new int [] {x, y})
- 시작점 (x, y)를 큐에 넣습니다.
- main문에서 (0,0)을 시작으로 했으니 초기 값은 (0,0)입니다.
- visited [x][y] = true;
- 시작점을 방문했음을 표시합니다.
- Queue <int []> queue = new LinkedList <>();
- 거리 초기화
- count = 1;
- 시작점부터 탐색을 시작하기 때문에 현재 위치의 거리를 1로 초기화하여 포함시켜줍니다.
- BFS 수행
- while (! queue.isEmpty()) {... }
- 큐가 비어있지 않은 동안 BFS를 반복합니다.
- int [] nowArr = queue.poll();
- 큐에서 현재 위치를 꺼내옵니다.
- int nowX = nowArr [0];
- int nowY = nowArr [1];
- 현재 위치의 좌표를 설정합니다.
- while (! queue.isEmpty()) {... }
- 목적지 도달 여부 확인
- if (nowX == N - 1 && nowY == M - 1) {... }
- 현재 위치가 목적지 (N-1, M-1)에 도달했는지 확인합니다.
- 도달했다면 count에 해당 위치의 거리를 저장하고 함수를 종료합니다.
- ➡️ 현재 위치에는 최단 거리가 존재합니다.
- if (nowX == N - 1 && nowY == M - 1) {... }
- 상하좌우 이동
- for (int i = 0; i < 4; i++) { ... }
- 상하좌우로 이동할 수 있는지 확인합니다.
- int nextX = nowX + dx [i];
- int nextY = nowY + dy [i];
- 다음 이동할 위치를 설정합니다.
- for (int i = 0; i < 4; i++) { ... }
- 이동 가능 여부 및 방문 여부 체크
- if (nextX >= 0 && nextX < N && nextY >= 0 && nextY < M) {... }
- 다음 위치가 미로 범위 내에 있는지 확인합니다. (범위 제한)
- if (map [nextX][nextY] == 1 &&! visited [nextX][nextY]) {... }
- 다음 위치가 이동 가능(1)하고,
아직 방문하지 않은 곳인지 확인합니다.
- 다음 위치가 이동 가능(1)하고,
- if (nextX >= 0 && nextX < N && nextY >= 0 && nextY < M) {... }
- 다음 위치 큐에 넣기 및 거리 업데이트
- queue.offer(new int [] {nextX, nextY});
- 다음 이동할 위치를 큐에 넣습니다.
- visited [nextX][nextY] = true;
- 다음 위치를 방문했음을 표시합니다.
- map [nextX][nextY] = map [nowX][nowY] + 1;
- 다음 위치의 거리를 현재 위치의 거리 + 1로 업데이트합니다.
- queue.offer(new int [] {nextX, nextY});
참고 ❗️
큐에 요소를 추가할 때 add()와 offer()는 기본적으로 비슷한 기능을 제공하지만, 큐에서는 offer 메서드를 사용하는 것이 권장됩니다.
이는 큐에 요소를 추가할 때 발생할 수 있는 예외 상황을 처리하는 방식에서 차이가 있기 때문입니다.
이해를 돕기 위해서 그림을 기반으로 추가 설명을 해보겠습니다.
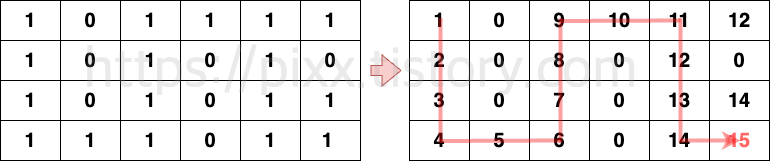
위 그림은 입력 예제 1번을 그림으로 표현한 것입니다.
앞서 설명한 "BFS동작 방식"을 기반으로 map에는 현재 위치까지 도달할 수 있는 최단 거리가 저장됩니다.
11에서 오른쪽과 아래 방향으로 이동이 가능하기 때문에 두 군데에 현재 위치 11의 +1 값인 12를 저장하게 됩니다. 이는 한 번에 여러 개의 이동 가능한 위치가 큐에 저장될 수 있습니다. 따라서 13에서 똑같이 두 방향으로 이동이 가능하기 때문에 13 + 1 = 14가 저장되고, 마지막으로 (N-1, M-1) ➡️(3,5)의 값인 15가 최단 거리가 됩니다.
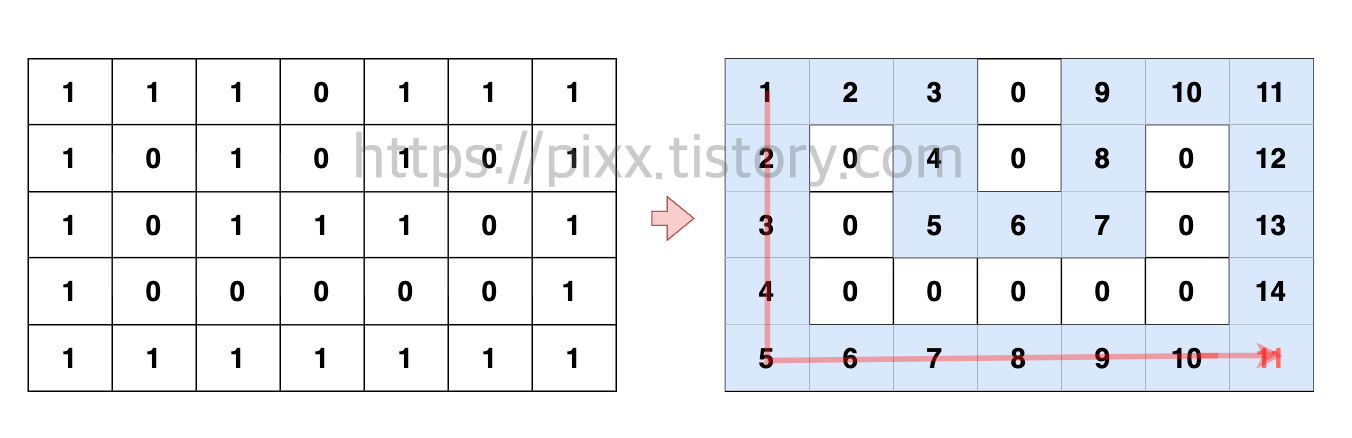
위 그림과 같은 케이스에서 약간 혼동되는 부분이 있을 것 같습니다.
최단 경로가 11이라는 것은 알 것 같은데 15가 될 수도 있는 것이 아닌가❓ 이런 의문이 들 수 있습니다.
하지만 BFS에서는 각 위치를 큐에 넣고 빼면서 탐색을 진행합니다.
따라서 여러 경로가 동시에 처리될 수 있지만, 가장 먼저 목적지에 도달한 경로가 해당 위치에 최단 거리를 업데이트합니다.
예를 들어,
- (0,0)에서 출발하여 (4,6)에 도착하는 경로 A
- (0,0)에서 출발하여 (4,6)에 도착하는 경로 B
위와 같이 경로가 있을 때, 먼저 도착한 경로가 (4,6)에 최단 거리를 11로 설정하고 배열에 저장됩니다.
이러한 방식으로, 이미 최단 경로에 도달한 위치는 그 이후의 경로들이 거리를 더 증가시키려 해도 무시됩니다. 따라서 BFS 탐색이 종료될 때 배열에는 각 위치까지의 최단 거리가 저장됩니다.
5 7
1110111
1010101
1011101
1000001
1111111
따라서 실제 입력이 위와 같이 입력된다면, 실제 미로는 아래와 같이 형성되게 됩니다. 따라서 (N-1, M-1) ➡️ (5,7)에 최단거리가 먼저 도달하기 때문에 count에 11가 저장되게 됩니다.

참고❗️
[자료구조 JAVA] 선형 구조 큐(Queue) 클래스 알아보기 ✔
Java를 활용하다 보면 데이터를 순차적으로 처리하거나, 특정 순서에 따라 데이터를 관리해야 할 때가 있습니다. 이때 사용할 수 있는 자료구조가 큐(Queue)입니다. 이 글에서는 Java의 큐(Queue)에
pixx.tistory.com
'Coding Test > 백준' 카테고리의 다른 글
| [백준] 2 x n 타일링 (동적 계획법, DP, 11726번, Java) (0) | 2024.07.13 |
|---|---|
| [백준] 수 찾기 (이진 탐색 , Binary Search, Buffer, sort(), 1920번, Java) (0) | 2024.07.09 |
| [백준] 피보나치 함수 (DP, 동적 계획법, 1003번, Java) (1) | 2024.07.08 |
| [백준] DFS와BFS (1260번, Java) (1) | 2024.07.05 |
| [백준] 연결 요소의 개수 (BufferedReader, DFS, 11724번, Java) (0) | 2024.07.03 |
