문제설명

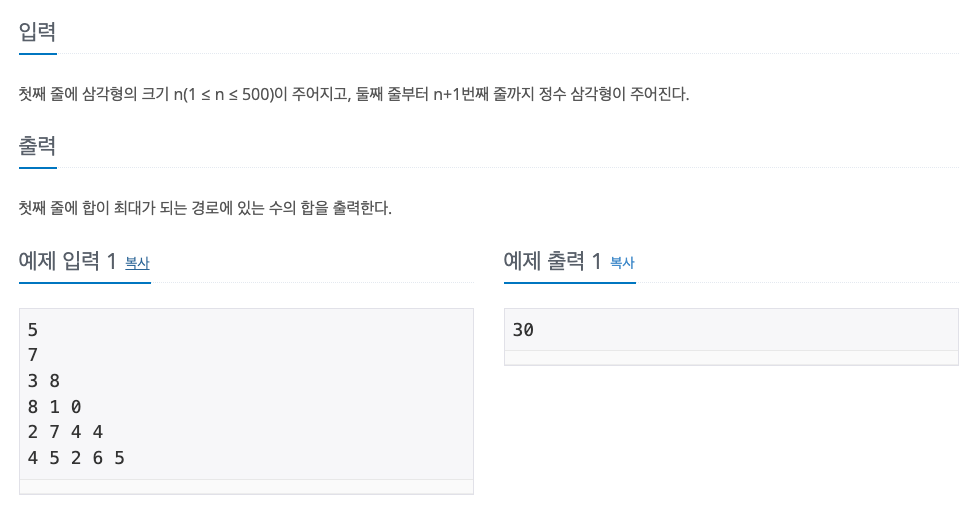
입력 & 출력
나의 풀이
문제 접근 방법
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
"백준 - 정수 삼각형"문제는 위와 같은 정수 삼각형에서 맨 위층에서 시작해서, 아래에 있는 수를 선택하여 마지막 레벨까지 도착했을 때 최대 합을 구하는 문제입니다. 이 때 아래에 있는 수는 왼쪽 대각선 또는 오른쪽 대각선만 선택할 수 있습니다.
이 문제를 해결하기 위한 핵심은 동적 계획법 (DP)을 사용하는 것입니다. 삼각형에서 각 정점마다 그 위치까지 올 수 있는 최대 합을 계산하여, 결국 맨 아래까지 내려오면서 최대 합을 구하는 방식입니다.
[Algorithm] 동적 계획법(Dynamic Programming, DP, Java) 알아보기
동적 계획법 DP란❓ 동적 계획법은 프로그래밍 대회 문제에 가장 자주 출현하는 디자인 패러다임 중 하나로 1940년대 리처드 벨만이 사용하던 용어입니다. 주로 줄여서 DP라고 많이 말하며, 주
pixx.tistory.com
저는 Top-Down 방식과 Bottom-up 방식중 Bottom-up방식을 사용했습니다.
아래에서부터 위로 올라가며 각 경로의 합을 계산합니다. dp[i][j]는 i번째 행, j번째 열의 위치까지 올 수 있는 최대 합을 저장하는 방식입니다. 최종적으로 가장 큰 합은 dp[0][0]에 저장됩니다.

계산 과정
Step 1:
dp[4] = [4, 5, 2, 6, 5]- 맨 아래 행을 그대로 dp에 저장합니다.
- 맨 아래 행에서는
더 이상 합을 더할 다른 경로가 없기 때문에 그 자체가 최대 합입니다.
Step 2:
dp[3] = [7, 12, 10, 10]- Step 2: 그 위의 행들에서 내려올 수 있는 최대 합을 계산합니다.
- dp[3][0]: triangle[3][0] + 아래 두 값 중 더 큰 값
- 2 + max(4, 5) = 2 + 5 = 7
- dp[3][1]: triangle[3][1] + 아래 두 값 중 더 큰 값
- 7 + max(5, 2) = 7 + 5 = 12
- dp[3][2]: triangle[3][2] + 아래 두 값 중 더 큰 값
- 4 + max(2, 6) = 4 + 6 = 10
- dp[3][3]: triangle[3][3] + 아래 두 값 중 더 큰 값
- 4 + max(6, 5) = 4 + 6 = 10
- dp[3][0]: triangle[3][0] + 아래 두 값 중 더 큰 값
Step 3:
dp[2] = [20, 13, 10]- Step 3: 3번째 행에서 내려올 수 있는 최대 합을 계산합니다.
- dp[2][0]: triangle[2][0] + 아래 두 값 중 더 큰 값
- 8 + max(7, 12) = 8 + 12 = 20
- dp[2][1]: triangle[2][1] + 아래 두 값 중 더 큰 값
- 1 + max(12, 10) = 1 + 12 = 13
- dp[2][2]: triangle[2][2] + 아래 두 값 중 더 큰 값
- 0 + max(10, 10) = 0 + 10 = 10
- dp[2][0]: triangle[2][0] + 아래 두 값 중 더 큰 값
Step 4:
dp[1] = [23, 21]- Step 4: 2번째 행에서 내려올 수 있는 최대 합을 계산합니다.
- dp[1][0]: triangle[1][0] + 아래 두 값 중 더 큰 값
- 3 + max(20, 13) = 3 + 20 = 23
- dp[1][1]: triangle[1][1] + 아래 두 값 중 더 큰 값
- 8 + max(13, 10) = 8 + 13 = 21
- dp[1][0]: triangle[1][0] + 아래 두 값 중 더 큰 값
Step 5:
dp[0] = [30]- Step 5: 1번째 행에서 내려올 수 있는 최대 합을 계산합니다.
- dp[0][0]: triangle[0][0] + 아래 두 값 중 더 큰 값
- 7 + max(23, 21) = 7 + 23 = 30
- dp[0][0]: triangle[0][0] + 아래 두 값 중 더 큰 값
요약
- 각 행에서 가능한 두 경로 중 더 큰 값을 더하며, 맨 아래에서부터 위로 올라가며 계산합니다.
- 마지막으로 dp[0][0]에 저장된 값이 최종적으로 가장 큰 합입니다.
전체 코드

먼저 이번 문제의 핵심인 DP배열 부분을 집중적으로 설명하겠습니다.
삼각형 정수를 받아주고, Bottom-up 방식이기 때문에 맨 아래 행에서는 더 이상 합을 더할 다른 경로가 없기 때문에 그 자체가 최대 합입니다. 따라서 clone()메서드로 삼각형의 마지막줄을 복사해줍니다.
dp의 맨 마지막 줄은 이미 초기화를 했기 때문에, 그 윗 줄부터(n-2)부터 반복문을 순회해줍니다.
그리고 1번째 줄에는 1개의 원소가 있고, 2번째 줄에는 2개의 원소 ... 이런식으로 n줄에는 n개의 원소가 존재하기 때문에 i+1로 배열의 크기를 초기화해줍니다.
그리고 현재 위치와 아래의 숫자 중 큰 값을 더해줘서 dp 배열을 만들어나가면 최종적으로는 dp[0][0]에 최댓값이 들어가게 됩니다.

public class 87649974 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] triangle = new int[n][];
for (int i = 0; i < n; i++) {
triangle[i] = new int[i + 1];
for (int j = 0; j <= i ; j++) {
triangle[i][j] = sc.nextInt();
}
}
// dp 초기화
int [][] dp = new int[n][];
dp[n-1] = triangle[n-1].clone();
for (int i = n-2; i >= 0; i--) {
dp[i] = new int[i+1];
for (int j = 0; j <= i; j++) {
dp[i][j] = triangle[i][j] + Math.max(dp[i+1][j],dp[i+1][j+1]);
}
}
System.out.println(dp[0][0]);
}
}
BufferedReader 클래스를 사용하여 입력을 받아주거나 Scanner를 사용해서 입력을 받아줄 수 있는데, 확실히 BufferedReader클래스를 사용해서 입력을 받아주는 것이 빠르고 메모리도 적게 사용하는 것을 확인할 수 있습니다.
- 87649974
- Scanner 사용
- 87649463
- BufferedReader 클래스 사용
'Coding Test > 백준' 카테고리의 다른 글
| [백준, 1541번] 잃어버린 괄호 (Java) (0) | 2024.12.21 |
|---|---|
| [백준, 1912번] 연속합 (다이나믹 프로그래밍, DP, 수열, Java) (0) | 2024.12.21 |
| [백준, 1874번] 스택 수열 (스택, 수열, Java) (1) | 2024.12.20 |
| [백준 , 11053번] 가장 긴 증가하는 부분 수열 (수열, 동적계획법, 다이나믹 프로그래밍 DP, Java) (1) | 2024.12.18 |
| [백준, 1931번] 회의실 배정 (그리디 알고리즘 greedy, Java) (0) | 2024.12.17 |

