
두 점 사이의 거리 공식
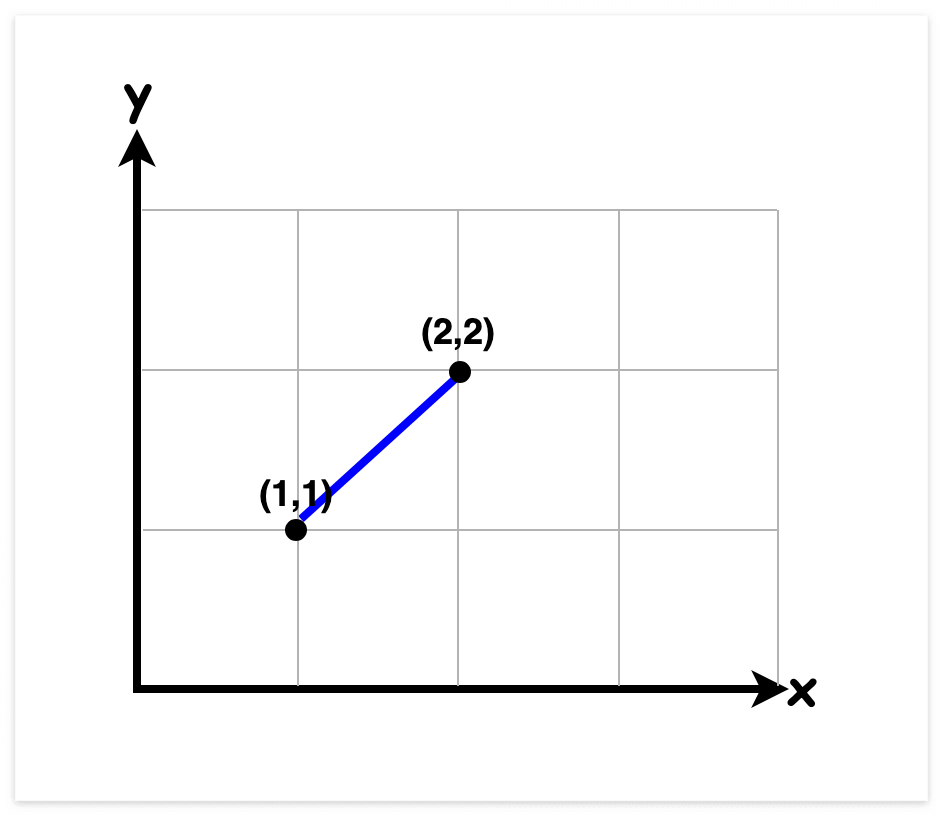
두 점 사이의 거리는 좌표평면 상에서 쉽게 구할 수 있습니다. 두 점 A(1,1)와 B(2,2)를 좌표평면 상에 그린다면 위와 같습니다.

두 점 A와 B를 지나는 직각삼각형을 그려보면, 밑변은 x좌표의 차이 (x₂-x₁), 높이는 y좌표의 차이 (y₂-y₁)가 됩니다. 이렇게 만들어진 직각삼각형의 빗변이 바로 우리가 구하고자 하는 두 점 사이의 거리입니다.
피타고라스 공식을 사용하여 두 좌표평면에서 두 점 A(x₁, y₁)와 B(x₂, y₂) 사이의 거리를 구하는 공식은 다음과 같습니다.
d = √[(x₂ - x₁)² + (y₂ - y₁)²]
두 원의 경우의 수
두 원을 평면에 그리면 다음과 같은 경우의 수로 그릴 수 있습니다.

두 원을 그린다면 위치 관계는 위와 같이 6개의 경우에 수로 떨어지게 됩니다.
두 원의 중심간의 거리
이제 우리가 알아본 두 점 사이의 거리 공식을 활용하면 두 원의 중심 사이의 거리도 쉽게 구할 수 있습니다. 두 원의 중심점을 각각 하나의 점으로 보고 똑같이 공식을 적용하면 됩니다.
두 원의 반지름을 각각 r₁, r₂라 하고, 두 원의 중심 사이의 거리를 d라고 할 때, 두 원의 위치 관계는 다음과 같이 6가지 경우로 나타낼 수 있습니다.

만나는 점의 개수 구하기
이처럼 두 원의 중심 사이의 거리 d와 반지름 r₁, r₂의 관계를 비교하면, 두 원의 위치 관계와 만나는 점의 개수를 쉽게 판단할 수 있습니다.
만약 A(1,1), B(2,2)가 있을 때 두 원의 위치 관계와 만나는 점의 개수를 구해보겠습니다.

두 원의 중심 사이의 거리를 구하는 공식 d = √[(x₂ - x₁)² + (y₂ - y₁)²] 에 좌표값을 대입하여 계산해보면
d = √[(2-1)² + (2-1)²] d = √[1 + 1] d = √2 ≈ 1.414
입니다. 이때 각 원의 반지름이 1로 동일하므로
- 두 반지름의 합
- r₁ + r₂ = 2
- 두 반지름의 차의 절댓값
- |r₁ - r₂| = 0
- 중심 사이의 거리
- d ≈ 1.414
위 관계를 보면 d < r₁ + r₂ 이고 d > |r₁ - r₂| 이므로, 두 원은 서로 두 점에서 만나게 됩니다.
