문제설명

입력 & 출력


나의 풀이
문제 접근 방법
"백준 - RGB 거리" 문제는 거리에 있는 집들을 R(red), G(green), B(blue)로 칠할 때, 다음 제약사항을 만족하면서 최소 비용으로 칠하는 문제입니다.
- 인접한 집은
같은 색으로 칠할 수 없음- 1번 집과 2번 집은 다른 색이어야 함
- N번 집과 N-1번 집은 다른 색이어야 함
- 2~N-1번 집은 양옆의 집과 다른 색이어야 함
현재 집을 칠하는 최소 비용이 이전 집의 색상 선택에 따른 최소 비용에 의존하므로, 문제를 작은 부분 문제로 나누어 해결할 수 있는 최적 부분 구조를 만족하며, 동일한 계산이 반복되는 중복되는 부분 문제 특성도 있어 다이나믹 프로그래밍으로 해결할 수 있습니다.
[Algorithm] 동적 계획법(Dynamic Programming, DP, Java) 알아보기
동적 계획법 DP란❓ 동적 계획법은 프로그래밍 대회 문제에 가장 자주 출현하는 디자인 패러다임 중 하나로 1940년대 리처드 벨만이 사용하던 용어입니다. 주로 줄여서 DP라고 많이 말하며, 주
pixx.tistory.com

예제 1번을 예로 들어 설명하자면, 위와 같은 RGB 거리에 집이 3개가 있고, 3개의 집을 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 다음과 같이 있습니다.
3
26 40 83
49 60 57
13 89 99
문제의 목표는 총 3개의 집을 칠해야할 때 최소 비용을 구하는 것입니다.

첫 번째 집은 이전에 비교할 대상이 없으므로, 해당 집을 각각의 색으로 칠했을 때의 비용이 그대로 최소 비용이 됩니다.
1 번째 집에서는 빨간색으로 칠했을 때 최소 비용이 됩니다.
두 번째 집부터는 이전 집과 같은 색으로 칠하지 않을 때를 고려해야합니다.

연속된 집은 같은 색으로 칠할 수 없다는 문제의 제약사항 때문에 2번째에서는 초록색과 파란색으로 칠할 수 있습니다.
따라서 이전 색상인 빨간색(26)과 현재 칠할 수 있는 초록색과 파란색 중 파란색으로 칠할 때 최솟값이 됩니다.
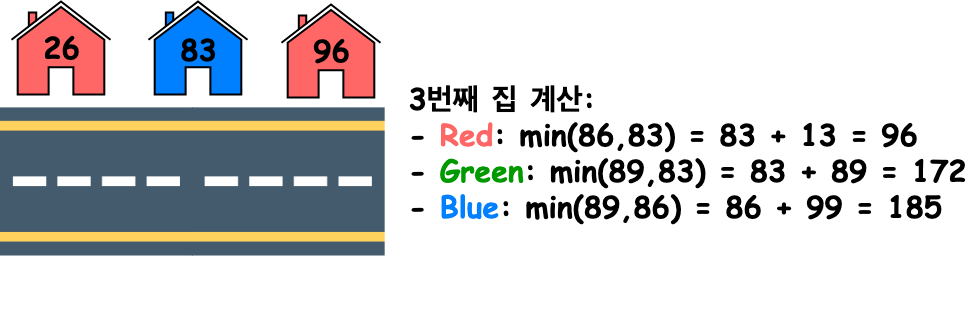
세 번째 집도 마찬가지로 이전 집의 색상이 파란색이기 때문에 현재 집에서 칠할 수 있는 색은 빨간색과 초록색입니다.
따라서 최솟값을 가지는 빨간색을 선택하게 됩니다.
전체 코드

문제의 핵심은 인접한 집을 같은 색으로 칠할 수 없다는 점입니다.
- 현재 집을 칠할 때는 이전 집의 색상을 제외한 나머지 색상들 중에서 선택해야 하고
- 각 단계의 최소 비용을 DP 배열에 저장하면서 진행합니다
- 마지막 집까지 칠한 후, DP 배열의 마지막 행에서 최솟값이 답이 됩니다.
즉, DP 배열의 각 행은 해당 집까지 칠했을 때 가능한 최소 비용을 저장하고 있으며, 이전 결과를 활용해 다음 단계의 최적해를 구하는 방식으로 문제를 해결합니다.
'Coding Test > 백준' 카테고리의 다른 글
| [백준, 14889번] 스타트와 링크 (백트래킹, 브루트 포스, Java) (0) | 2025.01.13 |
|---|---|
| [백준, 12865번] 평범한 배낭 (다이나믹 프로그래밍 : DP, 배낭 문제 : Knapsack, Java) (0) | 2025.01.11 |
| [백준, 1991번] 트리 순회 (트리, 재귀, Java) (0) | 2025.01.09 |
| [백준, 11279번] 최대 힙 (우선순위 큐, Java) (0) | 2025.01.07 |
| [백준, 2193번] 이친수 (다이나믹 프로그래밍 : DP, Java) (0) | 2025.01.06 |

