최장 공통 부분 수열(Longest Common Subsequence, LCS)란❓
최장 공통 부분 수열(LCS)은 두 수열이 주어졌을 때, 두 수열 모두의 부분 수열이 되는 수열 중 가장 긴 것을 말합니다.
여기서 중요한 점은 순서는 반드시 유지되어야 하지만, '연속된' 부분이 아니어도 된다는 것입니다.
부분 수열이란?
부분 수열은 주어진 수열에서 일부 원소를 선택해 원래 순서를 유지하면서 만든 수열입니다.
예를 들어, "ABCDE"의 부분 수열은 다음과 같습니다.
- "A"
- "ACE"
- "ABD"
- "ABCD" 등이 될 수 있습니다.
최장 공통 부분 수열 찾기
공통 부분 수열을 찾을 때의 핵심 규칙은 다음과 같습니다.
- 두 문자열에 모두 있는 문자여야 함
- 선택한 문자들의 순서가 두 문자열에서의 순서와 일치해야 함
- 문자열 1: "ABCD"
- 문자열 2: "ACED"
위 두 문자열에서 최장 공통 부분 수열(LCS)을 구해보겠습니다.
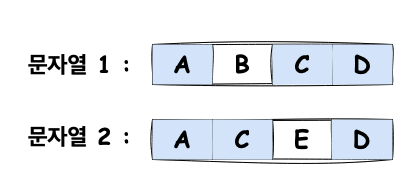
1단계 : 'A' 선택
문자열 1: A B C D
문자열 2: A C E D
↓
결과: A
- 두 문자열의 첫 번째 문자 'A'가 같음
- 첫 번째로 'A' 선택
2단계 : 'C 선택
문자열 1: A B C D
문자열 2: A C E D
↓ ↓
결과: A C
- 'A' 이후에 나오는 문자 중 공통인 'C' 발견
- 문자열1의 세 번째 'C'와 문자열2의 두 번째 'C' 매칭
- 두 번째로 'C' 선택
3단계 : 'D 선택
문자열 1: A B C D
문자열 2: A C E D
↓ ↓ ↓
결과: A C D- 'C' 이후에 나오는 문자 중 공통인 'D' 발견
- 두 문자열의 마지막 'D' 매칭
- 마지막으로 'D' 선택
최장 공통 부분 수열 DP로 해결하기 : Java
LCS는 대표적인 다이나믹 프로그래밍 문제입니다. 문제를 해결하는 과정을 단계별로 살펴보겠습니다.
[Algorithm] 동적 계획법(Dynamic Programming, DP, Java) 알아보기
동적 계획법 DP란❓ 동적 계획법은 프로그래밍 대회 문제에 가장 자주 출현하는 디자인 패러다임 중 하나로 1940년대 리처드 벨만이 사용하던 용어입니다. 주로 줄여서 DP라고 많이 말하며, 주
pixx.tistory.com
1. DP 테이블 정의
- dp[i][j] = 첫 번째 문자열의 i번째 위치까지와 두 번째 문자열의 j번째 위치까지의 LCS 길이
2. 점화식
if (str1[i] == str2[j]) {
dp[i][j] = dp[i-1][j-1] + 1
} else {
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
}- dp[i-1][j] = 첫 번째 문자열이 LCS에
포함되지 않는 경우 - dp[i][j-1] = 두 번째 문자열이 LCS에
포함되지 않는 경우 - dp[i-1][j-1] = 첫 번째, 두 번째 모두 LCS에 포함되는 경우
3. DP 테이블 구현과정
- 문자열 1: "SUNDAY"
- 문자열 2: "STURDY"
문자열 1: "SUNDAY" 와 문자열 2: "STURDY" 를 한 글자씩 비교를 합니다.
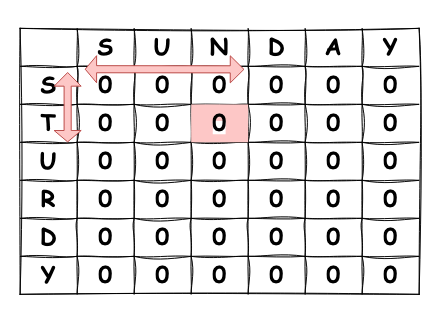
먼저 두 문자열의 길이만큼 LCS의 길이를 저장할 DP 테이블을 초기화해줍니다. 이때, 빨간색으로 표시된 위치는 두 문자열의 해당 위치에서 문자가 서로 일치하는지 비교하고, 일치한다면 LCS의 길이를 업데이트합니다.
즉, 현재는 "ST"와 "SUN"을 비교한 것 입니다.
첫 번째 행 채우기
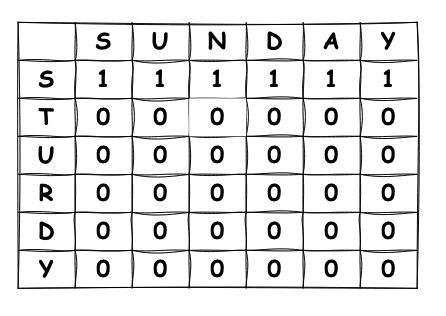
S가 같으므로 1을 채우고, 이후에는 같은 값이 없으므로 이전값을 유지합니다.
이 때 이전값을 유지하는 이유는 S와 S는 같으므로, LCS길이는 1이되고, 그 다음 'S'와 "SU"를 비교합니다.
- "S_"
- "SU"
위 경우에서 U와 비교할 대상이 없습니다. 이는 같지 않다는 말과 같고, LCS는 당연히 추가되지 않습니다.
따라서 비교하는 문자열이 같지 않다면 공통 부분 수열을 더 만들 수 없다는 의미이고, LCS의 길이는 이전값을 유지하게 됩니다.
S vs SU 와 S vs S는 둘다 LCS의 길이는 1이기 때문입니다. 이런 방식으로 각 위치에서 두 문자열을 비교하면서 LCS의 길이를 구해나갑니다.
두 번째 행 채우기
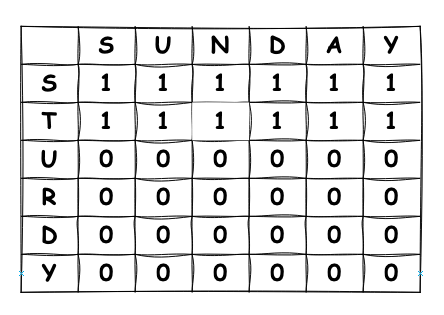
두 번째 행(T)에서는 같은 문자가 없으므로, 이전 최대값을 계속 유지합니다.
세 번째 행 채우기
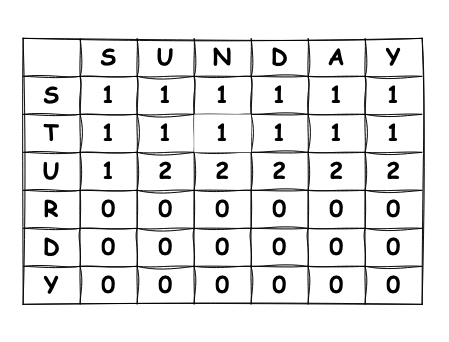
세 번째 행(U)에서는 U가 같으므로 대각선 LCS길이 +1을 해줍니다.
이때 대각선 위치의 값을 사용하는 이유를 살펴보면:
- "STU"와 "SU"를 비교할 때
- 대각선 위치는 "ST"와 "S"를 비교한 결과값을 가지고 있습니다.
- 여기에 두 문자열 모두에 같은 문자 U가 추가되었으므로
- 이전 LCS 길이에 1을 더해주면 현재 위치까지의 LCS 길이가 됩니다
따라서 대각선 위치의 LCS 길이가 1이었으므로, 여기에 1을 더해 2가 됩니다.
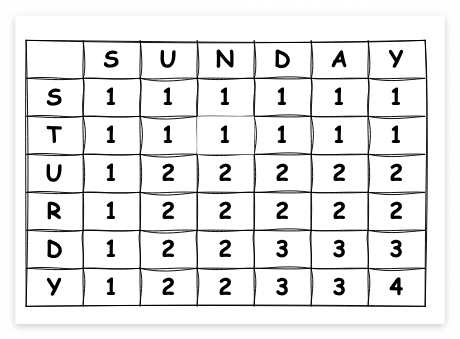
이런식으로 같은 값이면 대각선 LCS길이에서 +1을 해주고, 다른 값이면 이전 최대 LCS길이를 유지하면서 DP 배열을 채운다면 다음과 같이 최종적으로 DP 테이블이 완성이 됩니다.
최장 공통 부분 수열(LCS) 대표 문제
[백준, 9251번] LCS (LCS, 최장 공통 부분 수열, Java)
문제설명입력 & 출력나의 풀이문제 접근 방법"백준 - LCS" 문제는 최장 공통 부분 수열(LCS)알고리즘을 실제로 구현하는 문제입니다. LCS는 문제에서도 나와있듯이 두 수열이 주어졌을 때, 모두의
pixx.tistory.com
'Algorithm' 카테고리의 다른 글
| [Algorithm] 효율적인 그래프 탐색: 자바로 구현한 BFS 알아보기 (2/2) (0) | 2025.01.30 |
|---|---|
| [Algorithm] 0/1 배낭 문제(Knapsack) 알아보기 (0) | 2025.01.12 |
| [Algorithm] LIS : 가장 긴 증가하는 부분 수열 알고리즘 알아보기 (1) | 2024.12.18 |
| [Algorithm] 파스칼의 삼각형 알고리즘 구현하기 (Java) (1) | 2024.12.03 |
| [Algorithm] 백트래킹(Backtracking) 알고리즘 알아보기 (0) | 2024.11.27 |

