
▶every() 함수를 활용한 간단한 문제가 있어 정리해보고자 합니다.
문제설명
소수점 아래 숫자가 계속되지 않고 유한개인 소수를 유한소수라고 합니다. 분수를 소수로 고칠 때 유한소수로 나타낼 수 있는 분수인지 판별하려고 합니다. 유한소수가 되기 위한 분수의 조건은 다음과 같습니다.
기약분수로 나타내었을 때, 분모의 소인수가 2와 5만 존재해야 합니다.
두 정수 a와 b가 매개변수로 주어질 때, a/b가 유한소수이면 1을, 무한소수라면 2를 return 하도록 solution 함수를 완성해 주세요.
제한사항
- a, b는 정수
- 0 < a ≤ 1,000
- 0 < b ≤ 1,000
입출력 예 & 설명
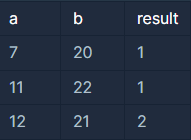
입출력 예 #1
- 분수 7/20은 기약분수입니다. 분모 20의 소인수가 2, 5 이기 때문에 유한소수입니다. 따라서 1을 return 합니다.
입출력 예 #2
- 분수 11/22는 기약분수로 나타내면 1/2입니다. 분모 2는 소인수가 2 뿐이기 때문에 유한소수입니다. 따라서 1을 return 합니다.
입출력 예 #2
- 분수 12/21는 기약분수로 나타내면 4/7입니다. 분모 7은 소인수가 7 이므로 무한소수입니다. 따라서 2를 return 합니다.
Hint
- 분자와 분모의 최대공약수로 약분하면 기약분수를 만들 수 있습니다.
- 정수도 유한소수로 분류합니다.
나의 풀이
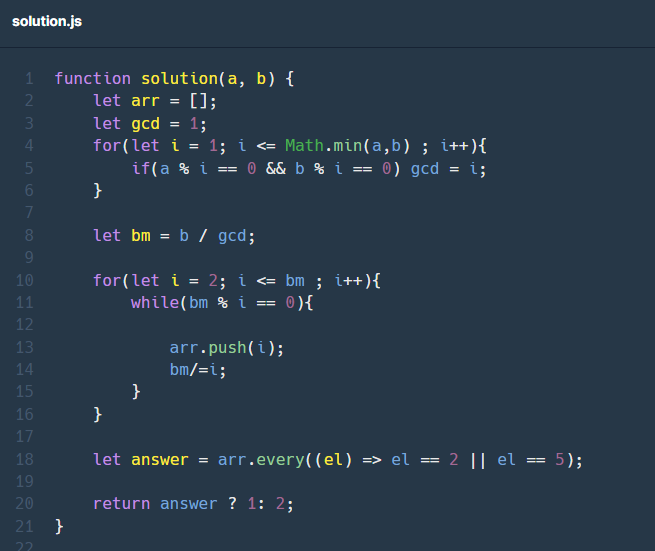
문제 설명에 앞서 저는 유클리드 호제법을 알지 못했기 때문에 나눗셈으로 최대공약수(gcd)를 구했습니다.
4번째 줄에서 최대공약수(gcd)를 구해줍니다.
기본 for문을 사용하여 1부터 최대공약수는 두 수보다 작거나 같기 때문에 범위를 이렇게 지정해 주었습니다.
만약 a와 b를 i로 나눴을 때 나머지가 0인경우 즉 공약수인 경우에 gcd에 넣어줍니다.
그렇다면 가장 나중에 값이 gcd값이 되는데 이 값이 최대공약수가 됩니다.
그리고 Hint에서 말했듯이 최대공약수로 분모를 나눠 기약분수의 분모로 만들어줍니다.
10번째 줄에서 분모의 소인수를 구해 arr배열에 넣어주어 소인수 배열을 만들어줍니다.
어떤 분수를 소수로 변환했을 때 유한소수인지 무한소수인지 구별할 수 있는 방법은 간단합니다.
분수를 기약분수로 고치고 소인수분해한 후 분모를 봤을 때
분모의 소인수가 2나 5밖에 없으면 유한소수, 2나 5 외에 다른 소인수가 존재하면 무한소수입니다.
그리고 위와 같이 소인수 분해한 분모가 2나 5 밖에 없으면 유한소수이기 때문에 every() 함수를 사용하여 소인수
배열에 2와 5만 존재하면 true값을 answer에 반환받습니다.
마지막으로 삼항연산자를 이용하여 최종적인 답을 반환하여 마무리했습니다.
다른 풀이
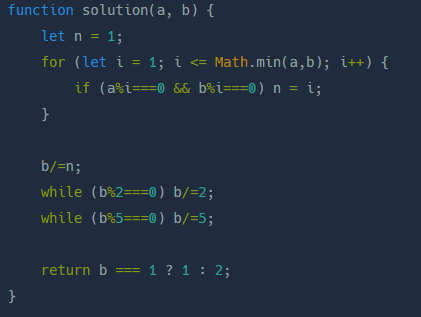
다른 풀이에서는 최대공약수는 "나의 풀이"와 동일하게 구해주고, 2와 5로 나눈 나머지 값이 0이 될 때까지 반복문을 실행하여 2와 5를 제외한 소수가 있는지 확인합니다.
그리고 return문에서 2와 5를 제외했으니깐 소인수가 2와 5 뿐인 유한소수는 존재하지 않게 되고, 2와 5 외의 값이 있는 무한소수는 값이 존재하기 때문에 삼항연산자를 사용하여 값이 있는지 체크 후 마무리했습니다.
저는 while문을 2번 쓰는 생각은 못했기 때문에 아주 좋은 코드 같습니다.
참고 ❗
최대 공약수를 구할 때 유클리드 호제법을 안다면 보다 쉽게 최대공약수(gcd)를 구할 수 있습니다.
혹시 저처럼 유클리드 호제법을 몰랐던 분이 계시면 아래의 링크를 통해 알아보실 수 있습니다!
function gcd(a, b) {
if (b === 0) return a;
return gcd(b, a % b);
}[Algorithm] 유클리드 호제법(최대공약수 gcd) 알아보기
1. 유클리드 호제법이란? 유클리드 호제법(- 互除法, Euclidean Algorithm) 유클리드(Euclid)에 의해 기원전 300년경에 발견된 가장 오래된 알고리즘 중 하나이며, 두 개의 정수 or 다수의 자연수에서 최대
pixx.tistory.com
[JavaScript] Array every(), some() 함수 알아보기
배열이 특정 조건을 만족하는지 확인하고자 하는 경우가 있습니다. 이때 사용하는 함수에는 every()와 some()이 있습니다. Array.every() Array.every() array.every(callbackFunction(currentValue, index, array), thisArg) cur
pixx.tistory.com
'Coding Test > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 특이한 정렬(JavaScript) (1) | 2024.03.12 |
|---|---|
| [프로그래머스] 안전지대 (JavaScript) (0) | 2024.03.11 |
| [프로그래머스] 다항식 더하기 (JavaScript) (0) | 2024.03.07 |
| [프로그래머스] 저주의 숫자 3 (JavaScript) (1) | 2024.02.28 |
| [프로그래머스] 직사각형 넓이 구하기 (JavaScript) (1) | 2024.02.25 |
