
이번 포스팅에서는 Java 알고리즘에서 필수적이라고도 말할 수 있는 DFS와 BFS에 대해서 알아보겠습니다.
자바를 활용하다 보면 그래프나 트리 구조를 탐색해야 할 때가 있습니다.
예를 들어, 네트워크 경로 탐색, 웹 크롤링, 게임 AI 에서의 경로 탐색 등 다양한 분야에서 이러한 탐색 알고리즘이 사용됩니다.
이때 사용할 수 있는 것이 DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색)입니다. 이 두 알고리즘은 그래프나 트리 구조에서 특정 노드를 찾거나, 모든 노드를 방문하는 데 유용합니다.
DFS(Depth-First-Search)란❓
Depth-First-Search를 번역해보면, 깊이 우선 탐색입니다. DFS(Depth-First Search)는 그래프 탐색 알고리즘 중 하나로, 이름에서 알 수 있듯이 깊이를 우선으로 탐색하는 방법입니다.
DFS알고리즘은 특정 경로로 탐색하다가 더 이상 진행할 수 없으면 다시 되돌아와서 다른 경로를 탐색합니다.
주로 "스택(Stack)" 자료구조를 사용하거나 "재귀 호출"을 통해 구현됩니다.
따라서 DFS알고리즘을 활용하기 위해서는 "그래프", "스택", "재귀 호출" 등의 개념이 선행되어야 합니다.

위 그림을 보면 시작 노드 1부터 시작하여 깊이를 우선으로 탐색하고, 4번 노드에서 더 이상 진행할 수 없기 때문에 다시 되돌아와서 계속해서 깊이를 우선으로 탐색하는 것을 볼 수 있습니다.
재귀호출을 사용한 DFS알고리즘
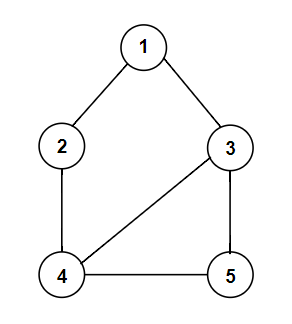
위와 같은 그림이 있을 Java의 배열과 재귀호출을 사용하여 표현하면 다음과 같습니다.
public class DFSExample {
// 정적 배열로 그래프를 인접 리스트로 표현
static int[][] graph = {
{}, // 0번 노드는 사용하지 않음
{2, 3}, // 1번 노드와 연결된 노드들
{1, 4}, // 2번 노드와 연결된 노드들
{1, 4, 5}, // 3번 노드와 연결된 노드들
{2, 3, 5}, // 4번 노드와 연결된 노드들
{3, 4} // 5번 노드와 연결된 노드들
};
static boolean[] visited = new boolean[graph.length]; // 방문 여부를 저장하는 배열
// DFS 함수
public static void dfs(int node) {
visited[node] = true; // 현재 노드를 방문한 것으로 표시
System.out.print(node + " "); // 방문한 노드 출력
// 현재 노드의 인접 노드를 재귀적으로 방문
for (int neighbor : graph[node]) {
if (!visited[neighbor]) {
dfs(neighbor);
}
}
}
public static void main(String[] args) {
System.out.print("DFS 탐색 순서: ");
dfs(1); // 시작 노드를 1로 설정하여 DFS 시작
}
}
실행결과
DFS 탐색 순서: 1 2 4 3 5
- 초기 상태:
- graph 배열은 각 노드와 연결된 노드들을 나타냅니다.
- visited 배열은 각 노드의 방문 여부를 추적하며, 초기에는 모든 값이 false입니다.
- main 함수에서 dfs(1)을 호출합니다.
- dfs(1) 호출:
- 노드 1을 방문하고 visited[1]을 true로 방문 처리합니다.
- 노드 1을 출력합니다: 1.
- 노드 1과 연결된 노드들(2, 3)을 순회합니다.
- dfs(2) 호출 (노드 1의 이웃 노드 2):
- 노드 2를 방문하고 visited[2]을 true로 설정합니다.
- 노드 2를 출력합니다: 1 2.
- 노드 2와 연결된 노드들(1, 4)을 순회합니다.
- 노드 1은
이미 방문했으므로, 다음 이웃인 노드 4로 이동합니다.
- dfs(4) 호출 (노드 2의 이웃 노드 4):
- 노드 4를 방문하고 visited[4]을 true로 설정합니다.
- 노드 4를 출력합니다: 1 2 4.
- 노드 4와 연결된 노드들(2, 3, 5)을 순회합니다.
- 노드 2는
이미 방문했으므로, 다음 이웃인 노드 3으로 이동합니다.
- dfs(3) 호출 (노드 4의 이웃 노드 3):
- 노드 3을 방문하고 visited[3]을 true로 설정합니다.
- 노드 3를 출력합니다: 1 2 4 3.
- 노드 3과 연결된 노드들(1, 4, 5)을 순회합니다.
- 노드 1과 4는
이미 방문했으므로, 다음 이웃인 노드 5로 이동합니다.
- dfs(5) 호출 (노드 3의 이웃 노드 5):
- 노드 5를 방문하고 visited[5]을 true로 설정합니다.
- 노드 5를 출력합니다: 1 2 4 3 5.
- 노드 5와 연결된 노드들(3, 4)을 순회합니다.
- 노드 3과 4는
이미 방문했으므로, 재귀 호출이 끝나고 반환합니다.
- 재귀 호출 반환:
- 모든 노드를 방문했으므로 재귀 호출이 반환됩니다.
- dfs(5)에서 dfs(3)로 반환하고, dfs(3)에서 dfs(4)로, dfs(4)에서 dfs(2)로, 그리고 최종적으로 dfs(2)에서 dfs(1)로 반환합니다.
- 노드 1의 다른 이웃 노드 3도 이미 방문했으므로 탐색이 끝납니다.
스택을 사용한 DFS알고리즘
import java.util.Stack;
public class DFSExample {
static int[][] graph = {
{}, // 0번 노드는 사용하지 않음
{2, 3}, // 1번 노드와 연결된 노드들
{1, 4}, // 2번 노드와 연결된 노드들
{1, 4, 5}, // 3번 노드와 연결된 노드들
{2, 3, 5}, // 4번 노드와 연결된 노드들
{3, 4} // 5번 노드와 연결된 노드들
};
static boolean[] visited = new boolean[graph.length]; // 방문 여부를 저장하는 배열
// DFS 함수 (스택 사용)
public static void dfs(int startNode) {
Stack<Integer> stack = new Stack<>();
stack.push(startNode);
visited[startNode] = true; // 시작 노드를 방문했다고 표시
while (!stack.isEmpty()) {
int node = stack.pop();
System.out.print(node + " "); // 방문한 노드 출력
// 인접 노드를 스택에 추가 (방문하지 않은 노드만 추가)
for (int neighbor : graph[node]) {
if (!visited[neighbor]) {
visited[neighbor] = true; // 인접 노드를 방문했다고 표시
stack.push(neighbor);
}
}
}
}
public static void main(String[] args) {
System.out.print("DFS 탐색 순서: ");
dfs(1); // 시작 노드를 1로 설정하여 DFS 시작
}
}
실행 결과
DFS 탐색 순서: 1 3 5 4 2
코드 진행 과정 설명
- 시작 노드 설정: dfs(1)을 호출하여 시작 노드를 1로 설정합니다.
- 스택 초기화: Stack<Integer> stack을 생성하여 시작 노드를 스택에 넣고, 시작 노드를 방문했다고 표시합니다 (visited[startNode] = true).
- 탐색 시작:
- 스택이 비어 있지 않은 동안 다음 과정을 반복합니다.
- 스택에서 노드 추출: stack.pop()을 사용하여 스택에서 가장 최근에 추가된 노드를 꺼냅니다. 이를 node라고 합니다.
- 노드 방문 처리: 현재 꺼낸 node를 방문한 것으로 표시하고, 출력합니다 (System.out.print(node + " ")).
- 인접 노드 탐색 및 스택에 추가:
- graph[node]를 통해 현재 노드와 인접한 노드들을 가져옵니다.
- 인접한 각 노드에 대해 아직 방문하지 않은 경우에만 다음 작업을 수행합니다.
- 방문하지 않은 인접 노드를 visited 배열에 표시하고, 스택에 추가합니다 (stack.push(neighbor)).
- 반복: 3단계로 돌아가 스택이 빌 때까지 반복합니다.
예시 실행
만약 시작 노드를 1로 설정하여 DFS를 실행한다면, 아래와 같은 과정을 거칠 수 있습니다:
- 시작 노드 1을 스택에 넣고 방문 표시합니다.
- 스택에서 1을 꺼내고 출력합니다. 인접 노드 2와 3을 스택에 추가합니다.
- 스택에서 3을 꺼내고 출력합니다. 인접 노드 4와 5를 스택에 추가합니다.
- 스택에서 5를 꺼내고 출력합니다. 이 때 인접 노드가 없으므로 추가할 노드가 없습니다.
- 스택에서 4를 꺼내고 출력합니다. 인접 노드가 1, 3, 5 중 방문하지 않은 1을 스택에 추가합니다.
- 스택에서 2를 꺼내고 출력합니다. 인접 노드가 1, 4 중 방문하지 않은 4를 스택에 추가합니다.
- 스택이 비어있으므로 종료합니다.
DFS탐색에서의 재귀 호출과 스택의 차이점
위 Java코드를 보면 같은 그래프에대해서 DFS탐색과정의 결과가 다른 것을 알 수 있습니다.
재귀 호출을 사용한 DFS 구현
재귀 호출을 사용한 DFS는 함수 호출 스택을 이용하여 구현됩니다. 주요 특징은 다음과 같습니다:
- 함수 호출 스택
- 재귀 함수가 호출될 때마다 호출 스택에 함수의 호출 정보가 저장됩니다.
- 깊이 우선 탐색
- 재귀 호출을 통해 가장 깊은 곳까지 탐색한 후, 되돌아오면서 다음 분기를 탐색합니다.
- 방문 순서
- 일반적으로 더 깊이 들어간 노드를 먼저 방문하게 되므로, 결과적으로 탐색 순서가 다를 수 있습니다.
스택을 사용한 DFS 구현
스택을 명시적으로 사용한 DFS는 반복문을 이용하여 구현됩니다. 주요 특징은 다음과 같습니다:
- 명시적 스택
- Stack 자료구조를 사용하여 노드를 관리하고 탐색합니다.
- 동일한 원리
- 재귀 호출을 사용한 DFS와 동일한 탐색 원리를 따릅니다.
- 방문 순서
- 스택에서 노드를 팝할 때의 순서에 따라 방문 순서가 결정됩니다.
- 일반적으로 인접 리스트의 역순으로 스택에 넣어서 꺼내(pop)므로, 탐색 순서가 재귀 호출을 사용한 것과 다를 수 있습니다.
따라서 구현 방식에 따라 스택을 사용한 DFS와 재귀 호출을 사용한 DFS의 탐색 순서가 다를 수 있습니다.
그래프의 구조는 동일하지만, 구현 방식에 의해 탐색 순서가 달라지는 이유입니다.
'Algorithm' 카테고리의 다른 글
| [Algorithm] KMP(Knuth-Morris-Pratt) 알고리즘이란 무엇일까❓ (문자열 비교) (2) | 2024.11.14 |
|---|---|
| [Algorithm] 이진 탐색 알고리즘 : 데이터 정렬과 검색 최적화 (Binary Search, Java) (0) | 2024.07.09 |
| [Algorithm] 그리디 알고리즘(탐욕법, greedy, Java) 알아보기 (0) | 2024.05.30 |
| [Algorithm] 동적 계획법(Dynamic Programming, DP, Java) 알아보기 (0) | 2024.05.29 |
| [Algorithm] 완전 탐색, 브루트 포스: 가장 단순한 알고리즘(Brute Force) 알아보기 (0) | 2024.05.23 |
