
문제설명
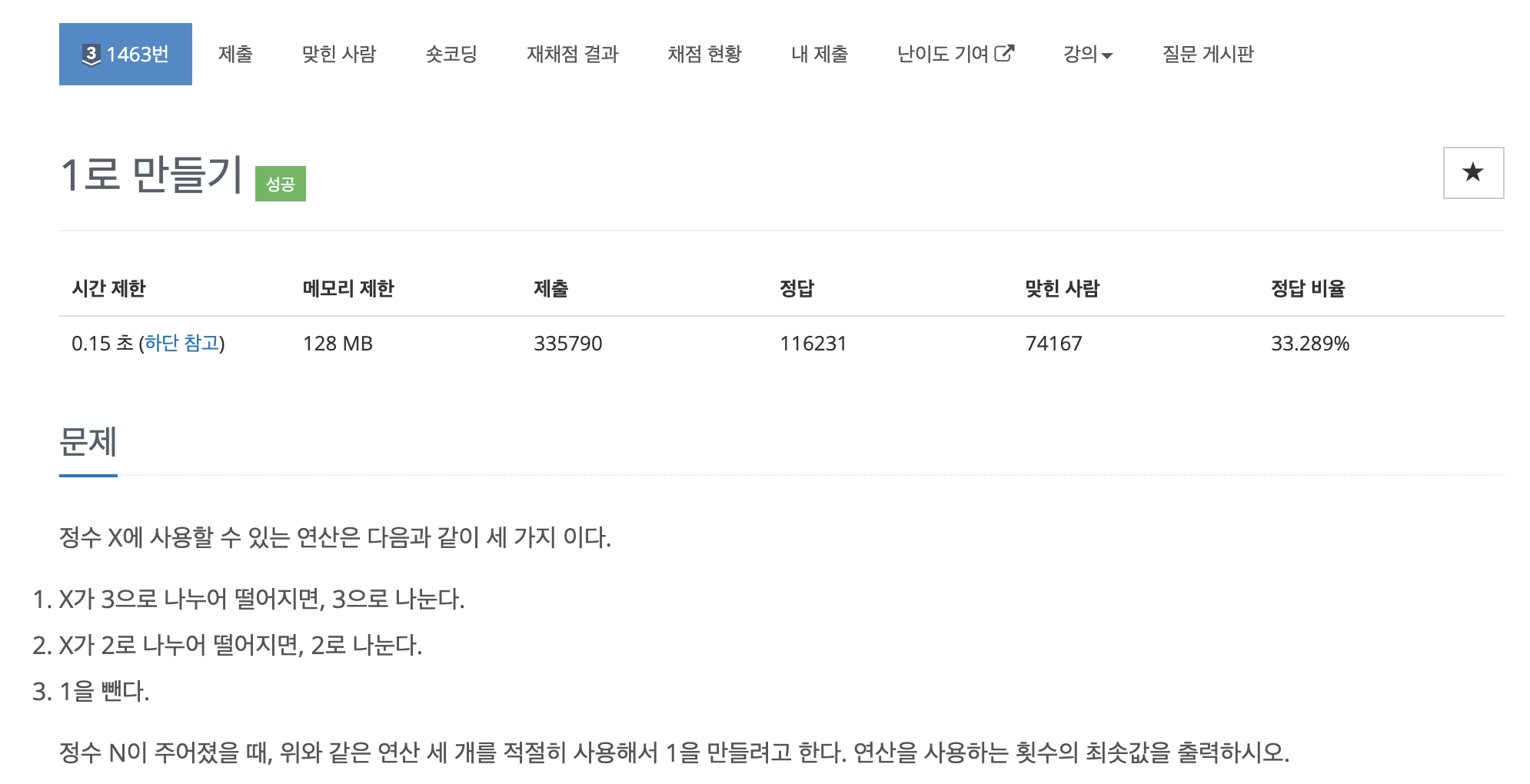
입력 & 출력

나의 풀이
이번 "백준 - 1로 만들기" 문제는 동적 계획법(DP)을 활용하여 해결할 수 있는 문제입니다.
[Algorithm] 동적 계획법(Dynamic Programming, DP, Java) 알아보기
동적 계획법 DP란❓ 동적 계획법은 프로그래밍 대회 문제에 가장 자주 출현하는 디자인 패러다임 중 하나로 1940년대 리처드 벨만이 사용하던 용어입니다. 주로 줄여서 DP라고 많이 말하며, 주
pixx.tistory.com
이 문제는 주어진 수 n을 1로 만들기 위해 최소 몇 번의 연산이 필요한지를 구하는 문제로, 가능한 연산은 다음과 같습니다
- n이 3으로 나누어 떨어지면 3으로 나눈다.
- n이 2로 나누어 떨어지면 2로 나눈다.
- n에서 1을 뺀다.
위 연산을 생각해본다면 결국 3가지의 연산으로 특정 숫자를 만들 수 있습니다. 예를 들어 n가 6 라면 각 연산해서 경우의 수를 살펴보겠습니다.
- 6 → 5 +1
- 5를 만들었던 연산에 +1 연산을 추가해서 6을 만들 수 있습니다.
- 즉, dp[5] + 1의 연산 횟수가 필요합니다.
- 3으로 나눠진다면 : 2 * 3 = 6
- 6은 3으로 나누어지므로, 6을 3으로 나누어 2가 되고, 2는 dp[2]에서 이미 계산된 최소 연산 횟수로 만들 수 있습니다.
- 즉, dp[3] + 1의 연산 횟수가 필요합니다.
- 2로 나누어진다면 : 3 * 2 = 6
- 6은 2으로 나누어지므로, 6을 2으로 나누어 3이 되고, 3은 dp[3]에서 이미 계산된 최소 연산 횟수로 만들 수 있습니다.
- 즉, dp[2] + 1의 연산 횟수가 필요합니다.
따라서 dp[6]은 위 3가지 경우에서 최소 연산을 선택하면 됩니다.
즉, 6을 구하는 연산은 당연히 여러가지가 있을 것이고, 연산은 3가지로 고정되어 있으니 3가지의 연산을 사용한 횟수 중 가장 적은 횟수가 정답이 됩니다.
또한 문제의 힌트에서 나와 있듯이 10을 구할 때에는 다음과 같은 경우의 수가 존재합니다.
- 10 → 9 → 3 → 1
- 10 → 5 → 4 → 2 → 1
- 10 → 6 → 3 → 1
이중에서 가장 횟수가 적은 연산인 3이 됩니다.
이해를 돕고자 그림을 준비했습니다. (ex : n = 10)

n이 10으로 주어졌을 때 dp배열의 초기값은 위와 같이 형성됩니다. 왜냐하면, dp[0] = 0 은 의미가 없고, dp[1] = 1은 2에서 1을 빼는 연산이 최소의 연산이기 때문입니다.
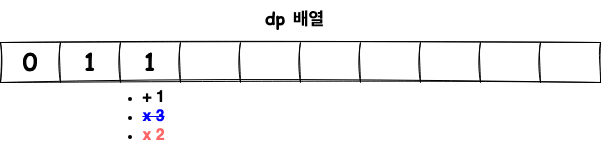
dp[3]은 위와 같이 두가지 방법이 가능합니다.
- 3으로 나누기: 3을 3으로 나누면 1이 되므로, dp[3] = dp[1] + 1 이 됩니다.
- 1 빼기: 3에서 1을 빼면 2가 되므로, dp[3] = dp[2] + 1이 됩니다.
이 두 가지 방법 중에서 더 적은 연산 횟수를 선택하게 됩니다. 즉, dp[3]은 다음과 같이 계산됩니다.
dp[3] = min(dp[2] + 1, dp[1] + 1)
이런식으로 입력 받은 n까지 진행하다보면 다음과 같이 dp배열이 만들어지게 됩니다.

전체 코드

1. DP 배열 초기화
- dp[i]는 숫자 i를 1로 만드는 최소 연산 횟수를 저장합니다.
- dp[0]과 dp[1]은 0으로 초기화하여 시작합니다. (0과 1은 이미 1이므로 연산이 필요 없음)
2. DP 배열 채우기
- for문을 사용해 2부터 X까지 각 숫자에 대해 최소 연산 횟수를 계산합니다.
- 기본 연산
- dp[num] = dp[num - 1] + 1 (항상 1을 빼는 연산은 가능)
- 3으로 나누어 떨어지면
- dp[num] = Math.min(dp[num], dp[num / 3] + 1)
- 2로 나누어 떨어지면
- dp[num] = Math.min(dp[num], dp[num / 2] + 1)
Math.max()메서드를 사용하여 가능한 연산 중 횟수가 적은 횟수를 저장하기 때문에 dp[X]에 저장된 값이 X를 1로 만드는 최소 연산 횟수입니다.
'Coding Test > 백준' 카테고리의 다른 글
| [백준, 11866번] 요세푸스 문제 0 (구현, 큐 Queue , Java) (1) | 2024.12.01 |
|---|---|
| [백준, 1018번] 체스판 다시 칠하기 (브루트 포스, Java) (0) | 2024.11.30 |
| [백준, 9012번] 괄호 (문자열, 스택, Java) (2) | 2024.11.28 |
| [백준, 15649번] N과 M(1) (백트래킹, Java) (0) | 2024.11.28 |
| [백준, 9655번] 돌 게임 (다이나믹 프로그래밍, DP, Java) (0) | 2024.11.25 |