
문제설명

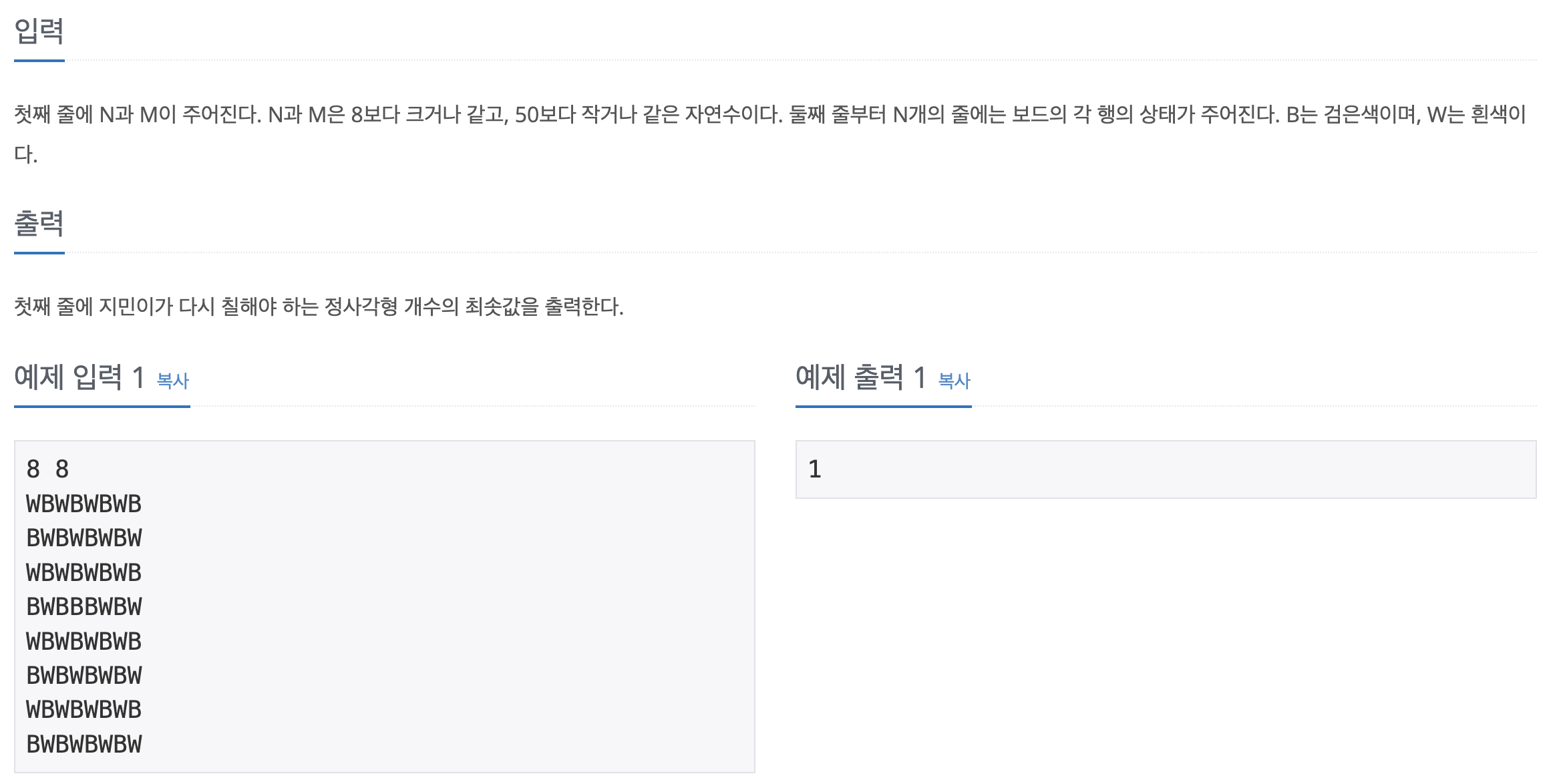
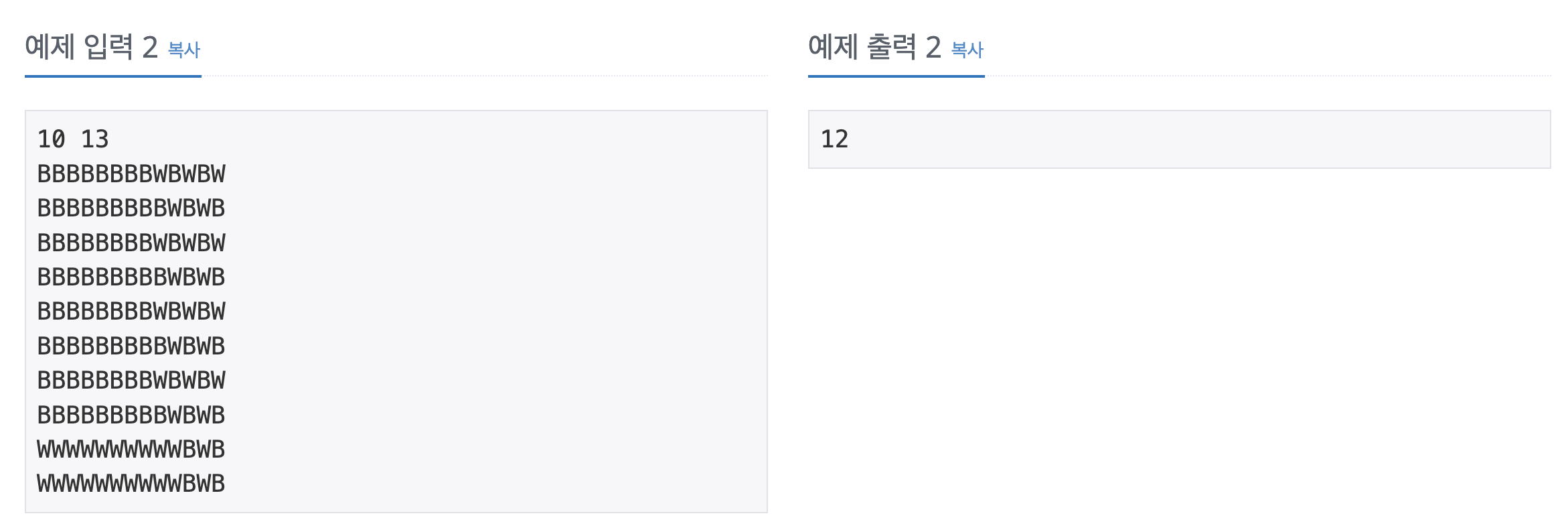
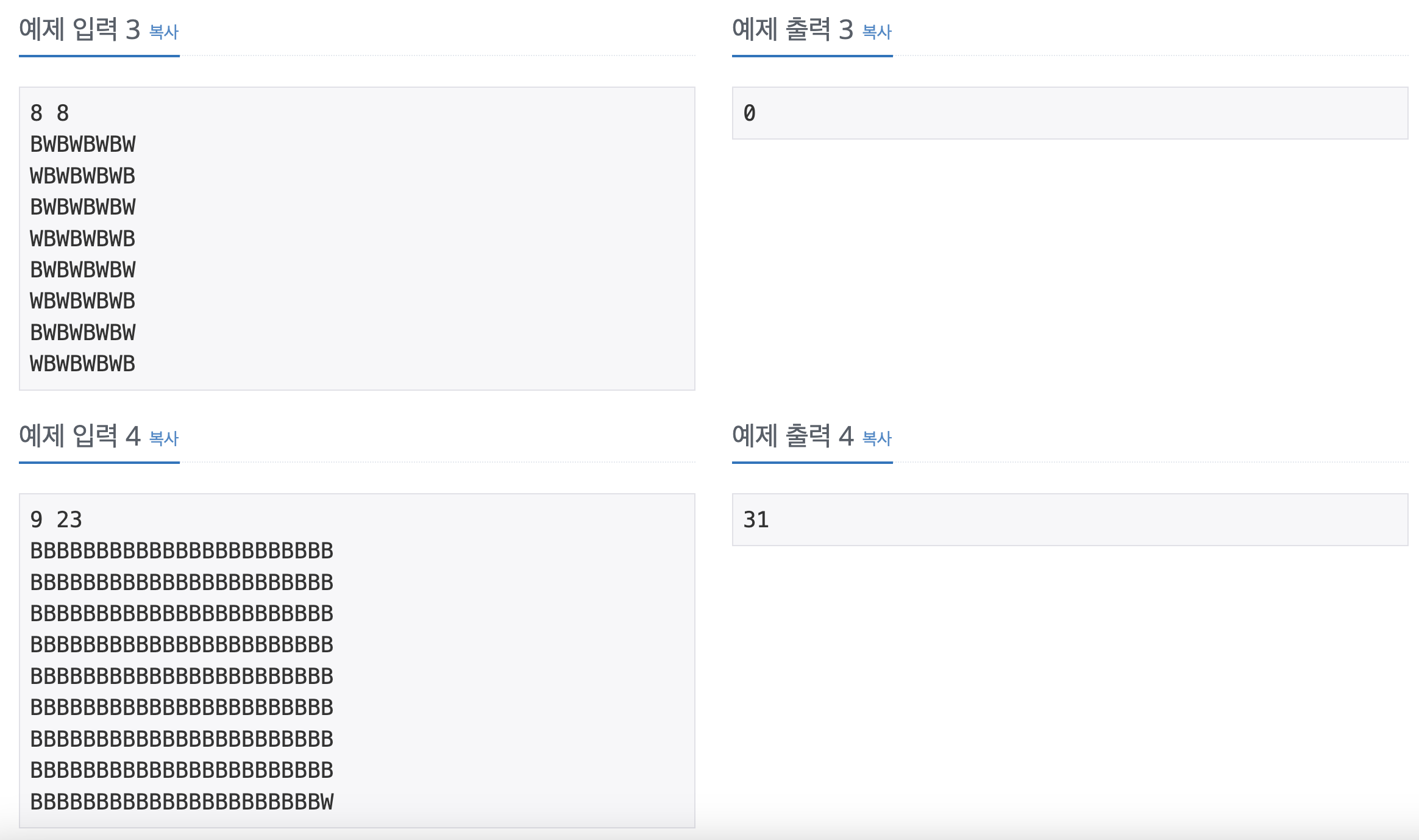
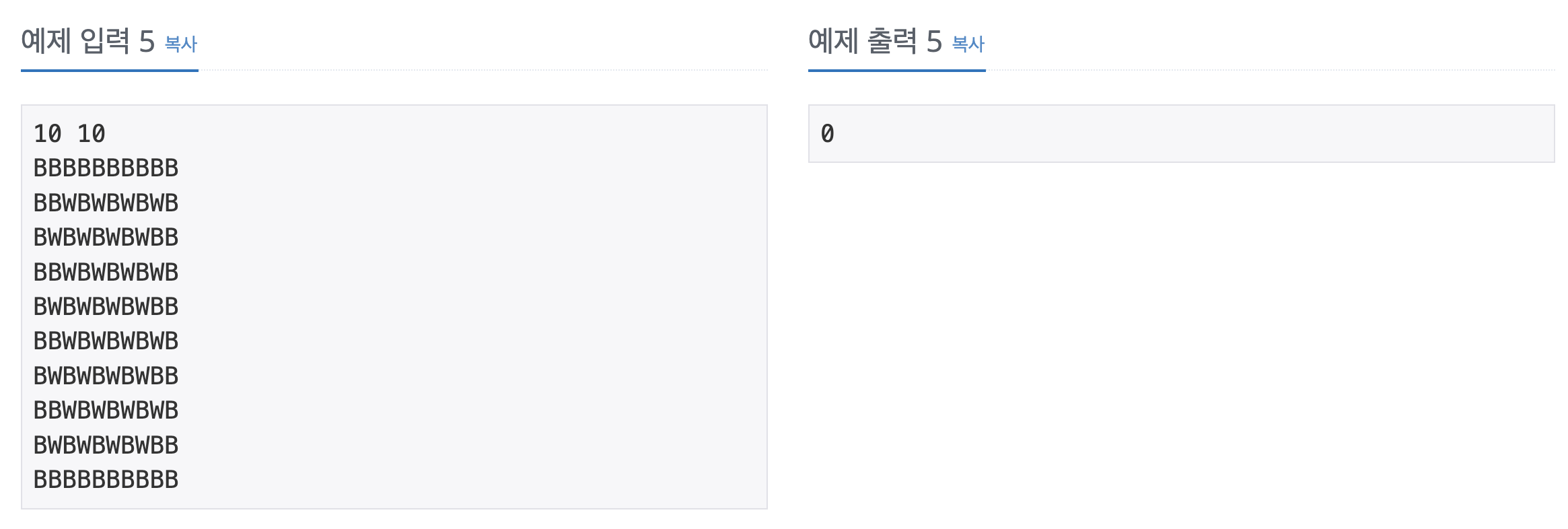
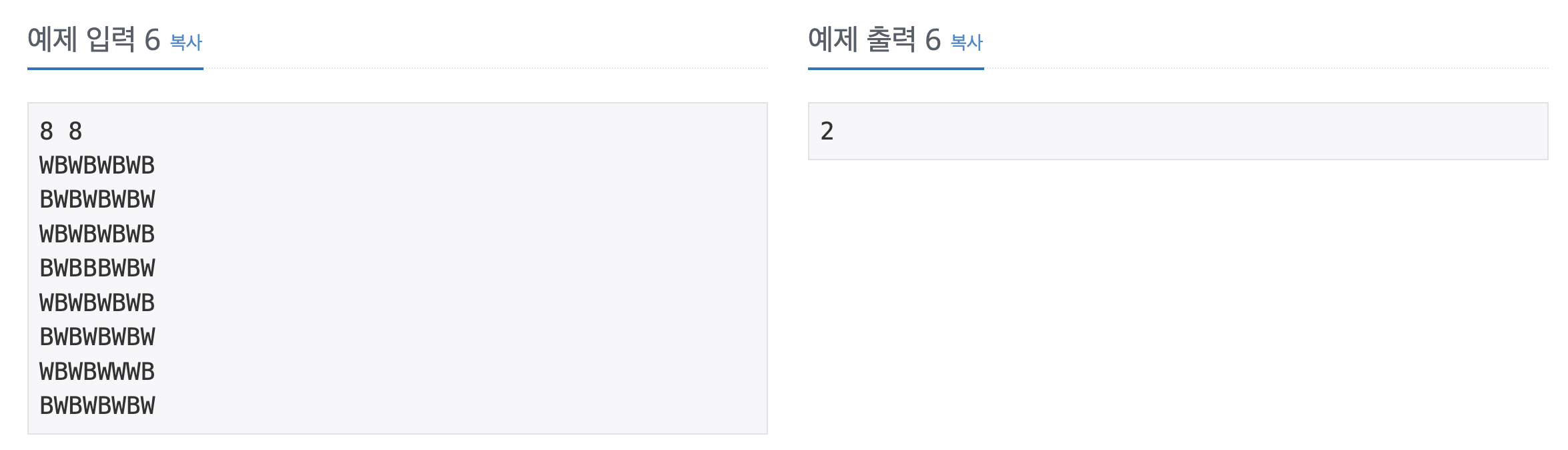
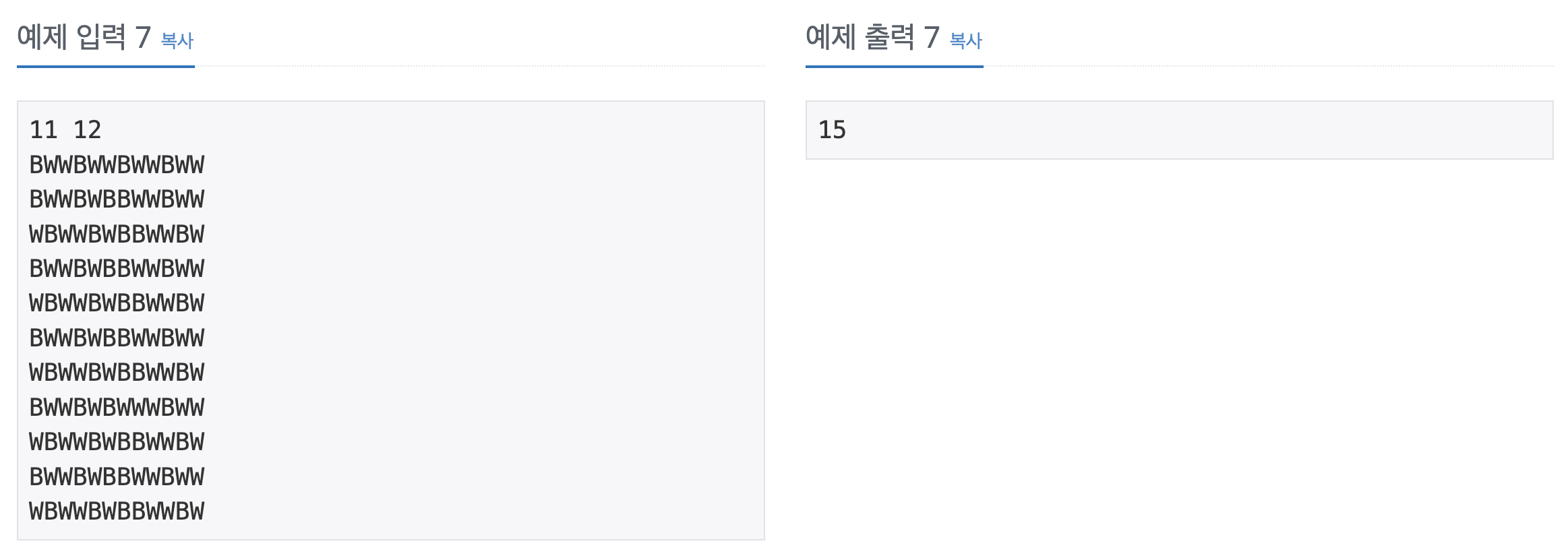
입력 & 출력
나의 풀이
이번 "백준 - 체스판 다시 칠하기" 문제는 간단히 말해 체스판이 주어졌을 때 8X8크기로 자르고, 체스판이 잘못 칠해져 있는 경우 다시 칠해야 하는 개수를 최소로 구하는 문제입니다.
브루트 포스 알고리즘을 사용하여 풀이한다면 문제 자체는 어렵지 않고 체스판을 8 X 8로 자르는 것이 포인트라고 생각합니다.
[Algorithm] 완전 탐색, 브루트 포스: 가장 단순한 알고리즘(Brute Force) 알아보기
한 사람이 단어를 생각하고 다른 사람이 그 단어를 추측하는 만약 "단어 맞추기" 게임을 한다면 추측하는 사람은 가능한 모든 단어를 시도하여 맞출 때까지 계속합니다. 예를 들어 추측하는 사
pixx.tistory.com
저는 다음과 같은 했습니다.
1. 체스판 8 x 8 영역 자르기
- 입력으로 주어지는 체스판은 8X8크기가 넘을 수 있기 때문에 가능한 8 X 8
시작위치로 잘라줍니다.
2. 다시 칠해야 하는 칸 계산

- 체스판은 문제에서 나와있듯이 두 가지 패턴(whiteBoard, blackBoard)이 있습니다.
- 두 가지 패턴과 비교하여 다시 칠해야하는 칸 수를 구해줍니다.
3. 최솟값 갱신
- 두 가지 패턴에 대해 계산된 칸 수 중 최솟값을 저장합니다.
말보다 그림으로 보는 것이 이해가 더 쉽기 때문에 예제 입력 2번 기준으로 설명하자면 다음과 같습니다.
10 13
BBBBBBBBWBWBW
BBBBBBBBBWBWB
BBBBBBBBWBWBW
BBBBBBBBBWBWB
BBBBBBBBWBWBW
BBBBBBBBBWBWB
BBBBBBBBWBWBW
BBBBBBBBBWBWB
WWWWWWWWWWBWB
WWWWWWWWWWBWB
그렇다면 해당 체스판은 8 X 8 보다 크기 떄문에 크기에 맞춰 잘라줘야 합니다. 이 때 이해하기 쉽도록 N과M을 row와 col로 부르겠습니다.
- 주어진 체스판에서 8x8로 자르려면, 시작할 수 있는 행(row)은 0, 1, 2입니다.
- i = 0부터 시작하면 0, 1, 2, ..., 7 번째 행을 자를 수 있습니다.
- i = 1부터 시작하면 1, 2, 3, ..., 8 번째 행을 자를 수 있습니다.
- i = 2부터 시작하면 2, 3, 4, ..., 9 번째 행을 자를 수 있습니다.
- 그래서 행(row)에 대한 시작 인덱스는 0, 1, 2 입니다.
- 주어진 체스판에서 8x8로 자르려면, 시작할 수 있는 열(col)은 0, 1, 2, 3, 4, 5까지입니다.
- j = 0부터 시작하면 0, 1, 2, ..., 7 번째 열을 자를 수 있습니다.
- j = 1부터 시작하면 1, 2, 3, ..., 8 번째 열을 자를 수 있습니다.
- j = 2부터 시작하면 2, 3, 4, ..., 9 번째 열을 자를 수 있습니다.
- j = 3부터 시작하면 3, 4, 5, ..., 10 번째 열을 자를 수 있습니다.
- j = 4부터 시작하면 4, 5, 6, ..., 11 번째 열을 자를 수 있습니다.
- j = 5부터 시작하면 5, 6, 7, ..., 12 번째 열을 자를 수 있습니다.
- 그래서 열(col)에 대한 시작 인덱스는 0, 1, 2, 3, 4, 5 입니다

따라서 위와 같이 범위를 벗어나지 않도록 체스판을 잘라야합니다. 그렇다면 8x8 체스판을 자를 때 시작점이 범위를 벗어나지 않도록 하기 위해서 다음과 같은 반복문을 통해 유효범위의 체스판을 잘라줍니다.

그러면 예제 입력2가 주어진다면 위와 같이 다시 칠해야하는 정사각형의 수는 12가 됩니다.
for (int i = 0; i <= N - 8 ; i++) {
for (int j = 0; j <= M - 8; j++) {
}
}전체 코드
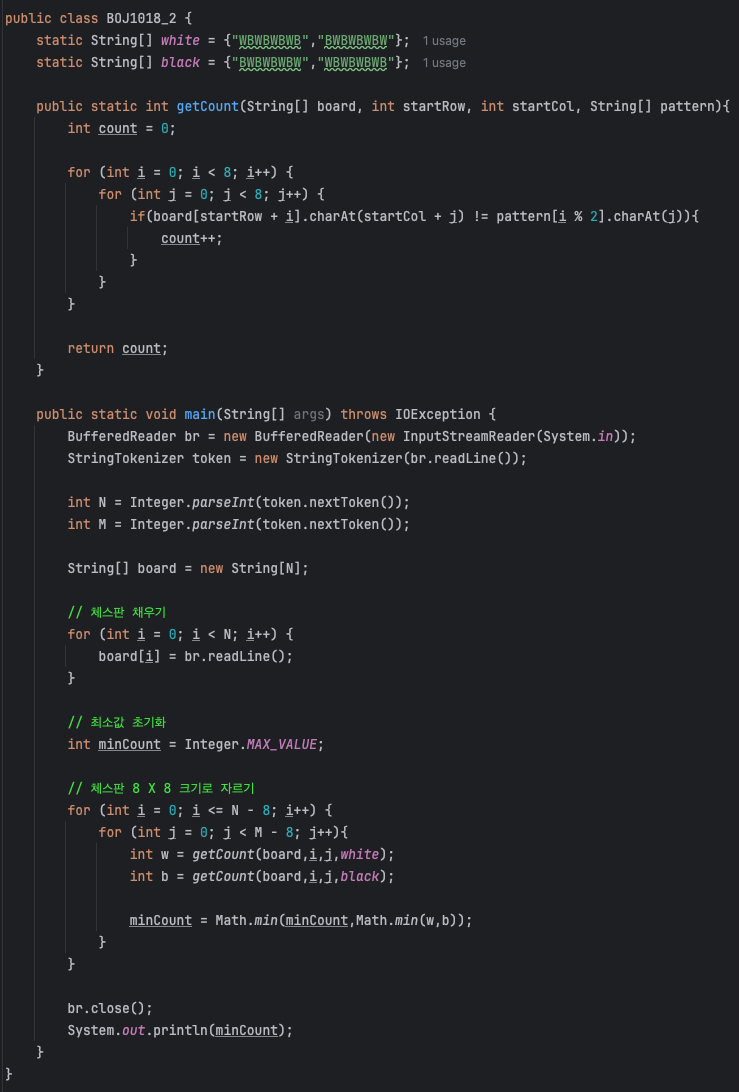
1. 전역 변수
먼저 체스판은 두 가지 패턴(whiteBoard, blackBoard)이 있기 때문에 좌측 상단이 하얀색으로 시작하는 whiteBoard 좌측 상단이 검은색으로 시작하는 blackBoard를 전역 변수로 체스판을 초기화해줍니다.
체스판은 반복되는 패턴을 가지므로, 두 패턴 모두 2줄씩만 초기화해도 충분합니다. 이후 나머지 연산(%)을 활용해 패턴을 반복적으로 비교하도록 구현하면 효율적으로 처리할 수 있습니다.
2. getCount() : 다시 칠해야 하는 칸의 수
시작하는 행(startRow)의 위치와 시작하는 열(startCol)의 위치, 비교할 패턴(black 또는 white), 그리고 비교할 체스판(board)을 매개변수로 받아, 8 x 8 크기의 부분 체스판에서 다시 칠해야 하는 정사각형의 개수를 계산합니다.
이 과정에서 체스판의 시작 위치(startRow)로부터 각 행을 탐색하며, 반복되는 패턴을 처리하기 위해 i % 2 연산을 사용하여 패턴의 행을 순차적으로 참조합니다.
3. main문
BufferedReader를 사용하여 입력을 받아주고, StringTokenizer를 사용하여 공백을 기준으로 N과 M을 읽어옵니다. 이후, 입력받은 N의 길이만큼 반복하며 체스판(board)을 초기화합니다.
다음으로, 체스판의 유효한 범위 내에서 8 x 8 크기로 잘라낼 수 있도록 반복문을 설정합니다. 이를 통해 범위를 벗어나지 않도록 처리합니다.
이후, getCount() 메서드를 호출하여 각 패턴(white, black)에 대해 다시 칠해야 하는 칸의 개수를 계산합니다. 그리고 Math.min() 메서드를 사용해 각 8 x 8 체스판에서의 최솟값을 구합니다.
'Coding Test > 백준' 카테고리의 다른 글
| [백준, 1010번] 다리 놓기 (수학, 다이나믹 프로그래밍, 동적 계획법: DP, Java) (0) | 2024.12.02 |
|---|---|
| [백준, 11866번] 요세푸스 문제 0 (구현, 큐 Queue , Java) (1) | 2024.12.01 |
| [백준, 1463번] 1로 만들기 (동적 계획법DP, Java) (0) | 2024.11.28 |
| [백준, 9012번] 괄호 (문자열, 스택, Java) (1) | 2024.11.28 |
| [백준, 15649번] N과 M(1) (백트래킹, Java) (0) | 2024.11.28 |