문제설명

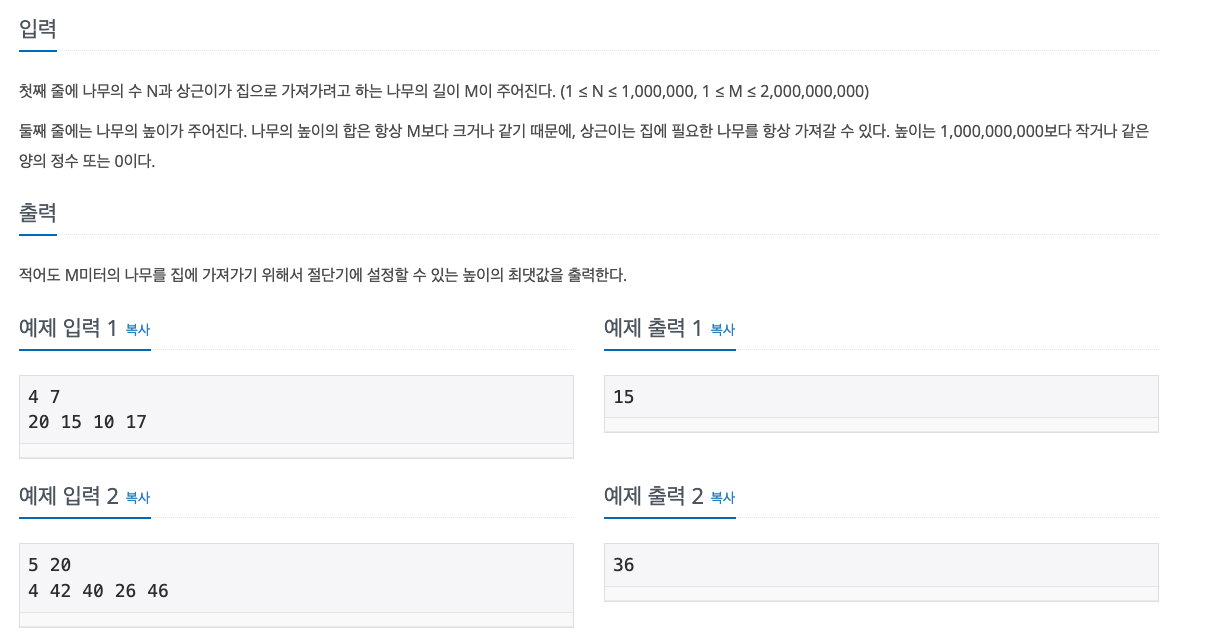
입력 & 출력
나의 풀이
문제 접근 방법
"백준 - 나무 자르기" 문제는 특정한 높이에서 나무를 잘라서 필요한 만큼의 나무를 얻을 수 있는지 여부를 결정할 수 있기 때문에 이진 탐색알고리즘을 사용한다면 효율적으로 풀이할 수 있습니다.
[Algorithm] 이진 탐색 알고리즘 : 데이터 정렬과 검색 최적화 (Binary Search, Java)
자바를 활용하다 보면 데이터 집합에서 특정 값을 빠르게 찾아야 할 때가 있습니다. 예를 들어, 정렬된 배열이나 리스트에서 원하는 값을 효율적으로 검색해야 하는 경우가 그렇습니다. 이러
pixx.tistory.com
이 때 상근이는 환경에 매우 관심이 많기 때문에, 나무를 필요한 만큼만 집으로 가져가야 합니다. 즉, 적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 출력해야 합니다.
따라서 M미터 이상의 나무를 집으로 가져가되, 환경을 고려하여 자를 수 있는 높이의 최댓값을 찾아야 합니다.
그림으로 정리하자면 다음과 같습니다.

위와 같이 나무가 있고, 필요한 나무의 길이가 7이라고 할 때 :
자를 수 있는 높이의 최댓값을 구해야 합니다. 이진 탐색 알고리즘을 사용할 것이기 때문에 left, right, mid 가 필요합니다.
left는 절단기 높이 H의 최솟값을 나타내고, right는 나무의 최댓값을 의미합니다.

문제에서 H (절단기 높이)는 "양의 정수 또는 0"이 가능하다고 명시되어 있습니다 따라서 절단기로 설정할 수 있는 가장 낮은 높이가 0입니다.
따라서 초기값을 left = 0, right = 20을 두고, 자를 수 있는 최대의 높이를 반으로 범위를 줄여가면서 찾아야 합니다.
처음은 높이가 10으로 설정되고, 자른다면 [10,5,10,7]의 길이로써 총 가져갈 수 있는 나무의 길이는 22입니다. M미터 이상을 가져갈 수 있기 때문에 절단기의 높이는 10으로 업데이트 합니다.
그리고 환경을 생각해야하는 최적의 값을 구하기 위해 left값을 오른쪽으로 이동하여 범위를 줄입니다. (10 + 1) ➡️ 11
다시 중간값을 계산(15)하고, 나무를 자르면 [5,0,0,2]의 길이로 총 가져갈 수 있는 나무의 길이는 7입니다. M미터 이상을 가져갈 수 있기 때문에 절단기의 높이는 15로 업데이트 합니다.

다시 중간값을 계산(18)하고, 나무를 자르면 [2,0,0,0]의 길이로 총 가져갈 수 있는 나무의 길이는 2입니다. 가져가야 할 길이(M)보다 작기 때문에 절단기의 높이를 낮춰야 합니다. 따라서 right값을 왼쪽으로 이동하여 범위를 줄입니다. (18 - 1) ⬅️ 17

다시 중간값을 계산(16)하고, 나무를 자르면 [4,0,0,1]의 길이로 총 가져갈 수 있는 나무의 길이는 5입니다. 가져가야 할 길이(M)보다 작기 때문에 절단기의 높이를 낮춰야 합니다. 따라서 right값을 왼쪽으로 이동하여 범위를 줄입니다. (16 - 1) ⬅️ 15
left > right가 되는 순간 반복문이 종료되고, 최종적으로 절단기의 최대 높이 15를 구할 수 있습니다.
전체 코드
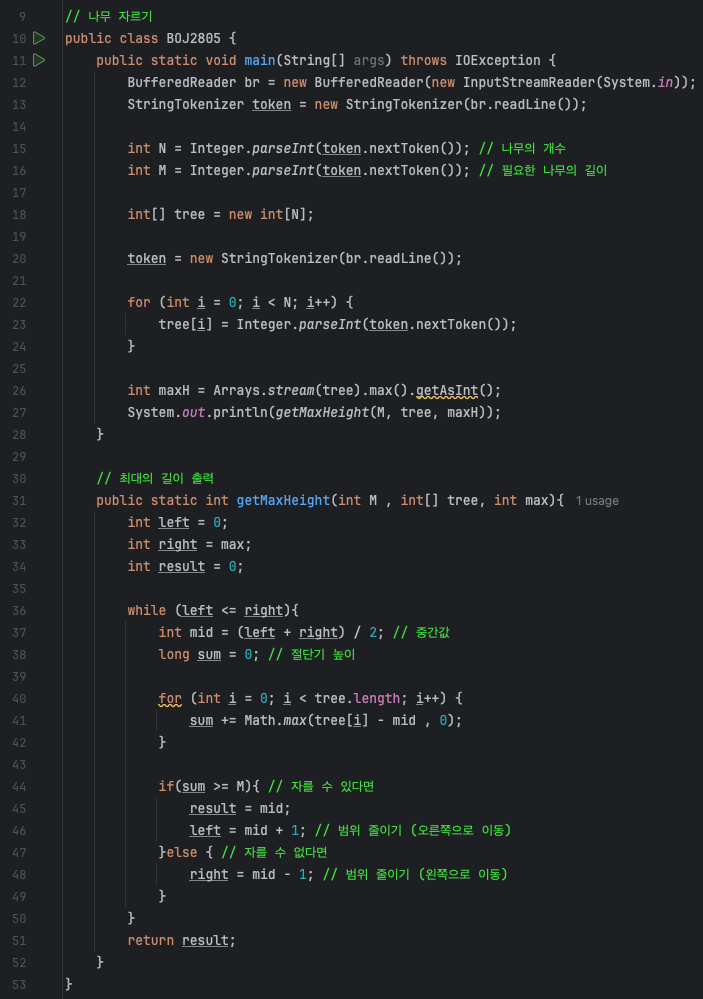
문제의 핵심은 M미터 이상의 나무를 집으로 가져가되, 환경을 고려하여 자를 수 있는 높이의 최댓값을 찾아야 합니다.
자를 수 있다면 즉, 가져가야 하는 나무의 길이M 이상이라면 일단 높이를 업데이트하고, 범위를 오른쪽으로 이동합니다. 그리고 자를 수 없다면 왼쪽으로 범위를 줄여가면서 최종적으로 left <= right가 될 때 반복문이 종료가 되고 저장되는 높이가 최댓값이 됩니다.
'Coding Test > 백준' 카테고리의 다른 글
| [백준, 2156번] 포도주 시식 (다이나믹 프로그래밍 : DP, 동적 계획법 , Java) (2) | 2025.01.01 |
|---|---|
| [백준, 1654번] 랜선 자르기 (이진 탐색, 이분 탐색, Java) (0) | 2024.12.31 |
| [백준, 1002번] 터렛 (수학, 기하학, Java) (1) | 2024.12.26 |
| [백준, 1541번] 잃어버린 괄호 (Java) (0) | 2024.12.21 |
| [백준, 1912번] 연속합 (다이나믹 프로그래밍, DP, 수열, Java) (0) | 2024.12.21 |

