문제설명

입력 & 출력
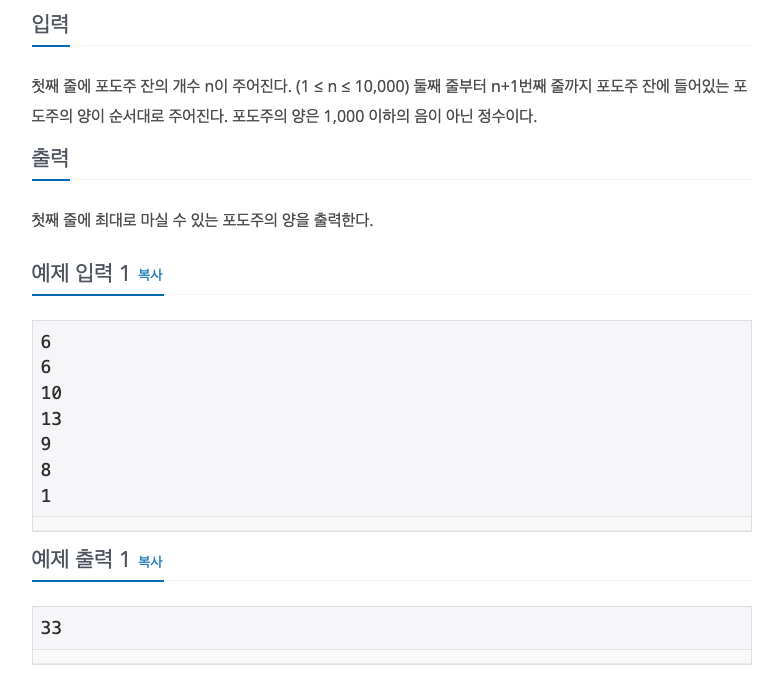
나의 풀이
문제 접근 방법
"백준 - 포도주 시식" 문제는 포도주가 1 ~ n개 있을 때 아래의 조건을 만족하는 가장 많은 양의 포도주를 마실 수 있는 양을 출력하는 문제입니다.
- 포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다.
- 연속으로 놓여 있는
3잔을 모두 마실 수는 없다.
즉, 순서대로 포도주를 마실때 최대의 포도주 양을 구하면 되는 문제입니다.
문제의 핵심은 연속해서 3잔을 마실 수 없을 때 최대의 포도주 양을 구하는 것이 기 때문에, 이 점을 고려해야합니다.
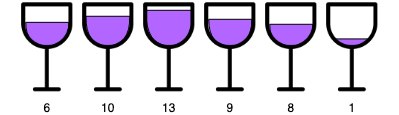
위와 같이 테이블에 연속된 포도주가 [6, 10, 13, 9, 8 ,1]이 있을 때 마실 수 있는 최대의 포도주의 양은 첫 번째, 두 번째, 네 번째, 다섯 번째 포도주 잔 을 선택하면 총 포도주 양이 33으로 최대로 마실 수 있습니다.
i번째 포도주를 마실 수 있는 경우의 수는 총 3가지가 있습니다.
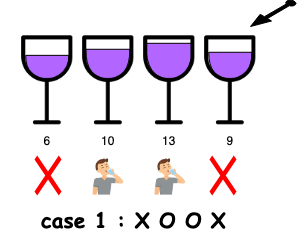
- case1: 현재 차례의 포도주를
마시지 않는경우 ➡️ (X O O X)- 이전까지 마신 포도주의 최대값을 그대로 사용
- 즉, i번째 포도주를 마시지 않고 이전 상태의 최적해를 유지

- case2: 이전 포도주를 건너뛰고 현재 포도주를 마시는 경우 ➡️ (O O X O)
- i-2까지의 최적해에 현재(i번째) 포도주를 마시는 경우
- i-1번째는 마시지 않아 연속 3잔을 피할 수 있음

- case3: 이전 포도주와 현재 포도주를 연속으로 마시는 경우 ➡️ (O X O O)
- i-3까지의 최적해에 i-1, i번째 포도주를 마시는 경우
- i-2번째는 마시지 않아 연속 3잔을 피할 수 있음
전체 코드

이번 문제는 다이나믹 프로그래밍 알고리즘을 사용하기에 적합한 문제입니다. 이 문제는 이전 위치들의 최적해를 재사용하여 현재의 최적해를 구할 수 있고, 이 과정에서 동일한 계산이 반복되므로 동적계획법을 사용하기에 적합합니다.
[Algorithm] 동적 계획법(Dynamic Programming, DP, Java) 알아보기
동적 계획법 DP란❓ 동적 계획법은 프로그래밍 대회 문제에 가장 자주 출현하는 디자인 패러다임 중 하나로 1940년대 리처드 벨만이 사용하던 용어입니다. 주로 줄여서 DP라고 많이 말하며, 주
pixx.tistory.com
또한 문제의 핵심인 '연속 3잔을 마실 수 없다'는 조건 때문에, 각 위치에서 가능한 경우의 수를 검토하여 최대값을 dp 배열에 저장해나가면, 최종적으로 dp 배열의 마지막 인덱스에 최대로 마실 수 있는 포도주의 양이 저장됩니다.
0, 1, 2번째 인덱스는 초기값을 세팅해야합니다. 특히 2번째 인덱스에서는 다음과 같은 경우의 수를 생각해야합니다.
- O O X
- O X O
- X O O
int case3 = dp[i-3] + wine[i-1] + wine[i];// O X O O
case3는 i-3까지의 최적의 합과 i-1번째, i번째 와인을 마시는 경우입니다.
여기서 'dp[i-1] + wine[i]'는 왜 사용할 수 없는지 살펴보겠습니다. dp[i-1]은 i-1까지의 최적의 합을 의미하는데, 이 경우 문제가 발생할 수 있습니다.
dp[i-1] + wine[i]
dp[i-1]이 이렇게 구성된 경우라면:
... X O O
↑ ↑
i-2 i-1
여기에 +wine[i]를 하면:
... X O O O
↑ ↑ ↑
i-2 i-1 i
연속 3잔을 마시게 되는 상황이 발생!
dp[i-3] + wine[i-1] + wine[i]
O X O O
↑ ↑ ↑ ↑
i-3 i-2 i-1 i
이렇게 i-2를 건너뛰어 연속 3잔을 마시는 것을 확실하게 피할 수 있습니다.
즉, 누적 합을 사용한다면 연속해서 3잔을 마실 수 있는 가능성이 있기 때문입니다!
'Coding Test > 백준' 카테고리의 다른 글
| [백준, 1927] 최소 힙 (우선순위 큐, Java) (1) | 2025.01.03 |
|---|---|
| [백준, 10844번] 쉬운 계단 수 (다이나믹 프로그래밍 : DP, Java) (2) | 2025.01.03 |
| [백준, 1654번] 랜선 자르기 (이진 탐색, 이분 탐색, Java) (0) | 2024.12.31 |
| [백준, 2805번] 나무 자르기 (이진 탐색, 이분 탐색, Java) (0) | 2024.12.30 |
| [백준, 1002번] 터렛 (수학, 기하학, Java) (1) | 2024.12.26 |

