728x90

누적 합(Prefix Sum) 알고리즘은 배열의 부분 합을 빠르게 계산하기 위한 유용한 도구입니다.
이는 특히 여러 번의 부분 합 계산이 필요한 상황에서 매우 효율적입니다. 이 글에서는 누적 합의 개념, 기본적인 구현 방법, 그리고 이를 활용한 문제 해결 방법에 대해 자세히 설명하겠습니다.
누적 합(Prefix Sum)란❓
누적 합은 주어진 배열의 각 원소까지의 합을 저장한 배열입니다. 수열 An에 대해서 구간[1, 1]의 합, 구간[1, 2]의 합, 구간[1, 3]의 합,..., [1, n]의 합을 누적 합이라고 합니다.
예를 들어, 배열 arr가 주어졌을 때,
prefixSum[i]는 arr [0]부터 arr [i-1]까지의 합을 의미합니다.
예를 들어, i = 3일 때 prefixSum[3] ➡️ 인덱스 0부터 인덱스 2까지의 누적 합을 의미합니다.

만약 위와 같은 길이 5의 배열이 있다면, 해당 배열의 누적 합 배열 prefixSum은 다음과 같이 계산됩니다
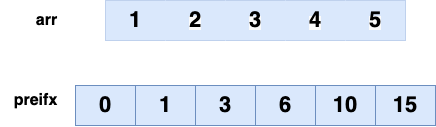
- prefix [0] = 0
- prefix [1] = 1
- prefix [2] = arr [0] : 1 + arr [1] : 2 ➡️ 3
- prefix [3] = arr [0] : 1 + arr [1] : 2 + arr [2] : 3 ➡️ 6
- prefix [4] = arr [0] : 1 + arr [1] : 2 + arr [2] : 3 + arr [3] : 4 = ➡️ 10
- prefix [5] = arr [0] : 1 + arr [1] : 2 + arr [2] : 3 + arr [3] : 4 + arr [4] : 5 = ➡️ 15
누적 합(Prefix Sum) 배열 생성
public int[] computePrefixSum(int[] arr) {
int n = arr.length;
int[] prefixSum = new int[n + 1];
for (int i = 0; i < n; i++) {
prefixSum[i + 1] = prefixSum[i] + arr[i];
}
return prefixSum;
}
이때 배열의 크기를 + 1 하는 이유는, 0~n번 인덱스의 구간 합도 구할 수 있게 만들기 위함입니다.
좀 더 자세히 말하자면 다음과 같습니다.
- 누적 합 배열의 초기 값 설정
- 누적 합 배열의 첫 번째 요소(prefixSum [0])를 0으로 설정합니다.
- 이는 1부터 시작하는 인덱스 체계를 사용하는 것이 편리하기 때문입니다. 예를 들어, 주어진 배열의 첫 번째 요소까지의 합을 계산할 때, prefixSum [1]을 사용할 수 있습니다.
- 구간 합 계산의 편의성
- 구간 합을 계산할 때, 시작 인덱스가 1인 경우와 0인 경우의 차이를 없애기 위함입니다.
- 예를 들어, 배열의 1번째 요소부터 3번째 요소까지의 합을 계산할 때, prefixSum [3] - prefixSum [0]을 사용하여 계산할 수 있습니다. 이는 인덱스 체계를 맞추는 데 도움이 됩니다.
누적 합(Prefix Sum)을 이용한 구간합 계산
누적 합을 이용하면 구간 합을 O(1) 시간에 계산할 수 있습니다.
예를 들어, 배열 arr에서 구간 [a, b]의 합을 계산하려면, prefixSum [b] - prefixSum [a-1]을 구하면 됩니다.
public int rangeSum(int[] prefixSum, int a, int b) {
return prefixSum[b] - prefixSum[a - 1];
}
❗️구간 합(Range Sum)
➡️ 배열이나 리스트의 연속된 부분 집합의 합을 의미합니다.
누적 합의 장점
1. 효율성
- 빠른 구간 합 계산
- 누적 합 배열을 사용하면 배열의 임의 구간 합을 O(1) 시간 복잡도로 계산할 수 있습니다.
- 이는 기본적으로 O(n)이 걸리는 구간 합 계산을 획기적으로 빠르게 만들어줍니다.
- 전처리 시간
- 누적 합 배열을 생성하는 데 O(n)의 시간이 소요됩니다.
- 이는 초기 한 번만 계산하면 되므로 전체적인 효율성을 크게 향상합니다.
2. 구현의 간단함
- 쉬운 구현
- 누적 합 배열을 생성하고 이를 사용하는 방법은 비교적 단순하며, 복잡한 자료
구조나 알고리즘을 필요로 하지 않습니다.
- 누적 합 배열을 생성하고 이를 사용하는 방법은 비교적 단순하며, 복잡한 자료
- 간단한 코드
- 누적 합을 활용한 코드는 비교적 짧고 간결하여 유지보수가 용이합니다.
3. 다용성
- 다양한 문제 해결
- 누적 합은 구간 합 계산 외에도 다양한 문제에 적용될 수 있습니다.
- 예를 들어, 특정 값 이상의 구간 찾기, 부분 배열의 최대 합 계산, 이진 탐색을 통한 특정 조건 만족하는 구간 찾기 등 여러 문제 해결에 응용될 수 있습니다.
- 확장 가능성
- 기본적인 누적 합 배열 외에도, 2차원 누적 합, 누적 곱, 차분 배열 등으로 확장하여 더 복잡한 문제를 해결할 수 있습니다.
4. 공간 효율성
- 작은 추가 메모리 사용
- 누적 합 배열은 입력 배열 크기보다 1만큼 큰 배열을 추가로 사용하므로, 메모리 사용량이 비교적 적습니다.
- 이는 메모리 제한이 있는 환경에서도 유용합니다.
이진 탐색(Binary Search) 예제
public class BinarySearchExample {
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid; // target found
}
if (arr[mid] < target) {
left = mid + 1; // search in the right half
} else {
right = mid - 1; // search in the left half
}
}
return -1; // target not found
}
public static void main(String[] args) {
int[] sortedArray = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19};
int target = 7;
int result = binarySearch(sortedArray, target);
if (result == -1) {
System.out.println("Target not found in the array.");
} else {
System.out.println("Target found at index: " + result);
}
}
}
실행 결과
Target found at index: 3
이진 탐색(Binary Search)의 장단점
장점
- 빠른 검색 속도
- 이진 탐색은 시간 복잡도가 O(log n)으로, 데이터 양이 많아질수록 선형 탐색(O(n))보다 훨씬 빠릅니다.
- 간단한 구현
- 구현이 비교적 간단하여 코드 작성이 용이합니다.
단점
- 정렬된 데이터 필요
- 이진 탐색을 사용하기 위해서는 데이터가 정렬되어 있어야 합니다. 데이터 정렬에 추가적인 비용이 발생할 수 있습니다.
- 동적 데이터 처리 어려움
- 데이터의 삽입, 삭제가 빈번하게 일어나는 경우, 매번 정렬을 유지해야 하기 때문에 비효율적일 수 있습니다.
'자료구조' 카테고리의 다른 글
| [JAVA] Deque (데크, 덱) 자료구조 알아보기 (0) | 2024.07.14 |
|---|---|
| [JAVA] 그래프 (Graph)알아보기 (0) | 2024.07.07 |
| [JAVA] HashSet 클래스 사용법 (중복 없는 데이터 집합) (0) | 2024.06.29 |
| [JAVA] HashMap_entrySet() : 데이터 접근과 반복을 간편하게 하는 방법(2/2) (0) | 2024.06.28 |
| [자료구조 JAVA] 우선순위 큐(Priority Queue) 클래스 알아보기 ✔ (0) | 2024.06.16 |
