
그래프는 많은 컴퓨터 과학 문제에서 필수적인 데이터 구조입니다.
그래프를 사용하면 복잡한 네트워크 구조를 모델링하고 다양한 문제를 해결할 수 있습니다.
예를 들어, SNS에서 친구 관계를 나타내거나, 도로망에서 최단 경로를 찾는 문제 등을 해결할 수 있습니다.
Graph란 ❓
Graph는 객체 또는 개체 간의 관계를 표현하는 자료구조입니다.
객체(Node)들 간의 연결(Egde)로 구성됩니다.
Graph의 정의
그래프는 두 가지 주요 구성 요소로 이루어집니다.
- 노드(정점, Vertex)
- 그래프에서 개별적인 객체 또는 노드를 나타냅니다.
- 간선(엣지,Edge)
- 노드 간의 연결을 나타내며, 노드 간의 관계를 정의합니다.
그래프는 노드와 간선의 집합으로 표현되며 다음과 같이 표현됩니다.
- G = (V,E)
- G : Graph
- V : 노드의 집합
- E : 간선의 집합
Graph의 종류
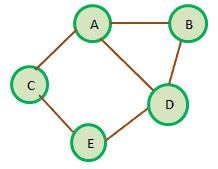
- 무방향 그래프 (Undirected Graph)
- 모든 간선이 양방향입니다.
- 즉, 간선 (u, v)는 u에서 v로도, v에서 u로도 갈 수 있습니다.
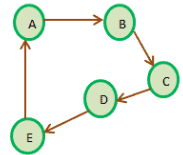
- 방향 그래프 (Directed Graph)
- 모든 간선이 단방향입니다.
- 즉, 간선 (u, v)는 u에서 v로만 갈 수 있습니다.
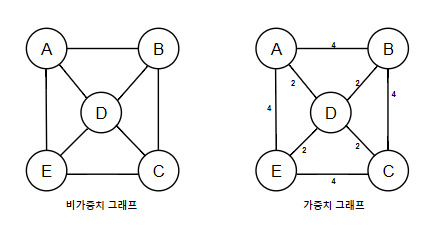
- 가중치 그래프 (Weighted Graph)
- 간선마다 가중치가 부여된 그래프입니다. 주로 최단 경로 알고리즘에서 사용됩니다.
- 비가중치 그래프 (Unweighted Graph)
- 모든 간선의 가중치가 동일한 그래프입니다.
그래프 표현
그래프를 표현하는 방법에는 주로 인접행렬(Adjacency Matrix)과 인접 리스트(Adjacency List) 두 가지가 있습니다.
인접 행렬(Adjacency Matrix)
인접 행렬은 2차원 배열을 사용하여 그래프를 표현하는 방법입니다.
행렬의 행과 열은 그래프의 노드를 나타내며, 특정 행과 열이 만나는 지점의 값은 두 노드 간의 연결을 나타냅니다.
- 장점
- 구현이 간단하고 직관적입니다.
- 간선의 존재 여부를 빠르게 확인할 수 있습니다.
- 단점
- 노드가 많을 경우 메모리 사용량이 많아질 수 있습니다.
- 간선이 적은 희소 그래프(Sparse Graph)에서는 비효율적입니다.
인접 리스트(Adjacency List)
인접 리스트는 각 노드에 연결된 다른 노드들을 리스트로 표현하는 방법입니다.
노드마다 리스트를 갖고 있으며, 리스트에는 해당 노드와 연결된 모든 노드가 포함됩니다.
- 장점
- 메모리 효율성이 좋습니다.
- 간선이 적은 희소 그래프(Sparse Graph)에서도 효율적입니다.
- 단점
- 간선의 존재 여부를 확인하는 데 시간이 더 걸릴 수 있습니다 (최악의 경우 O(V)).
이해를 위해 한가지 예를 들어보겠습니다.
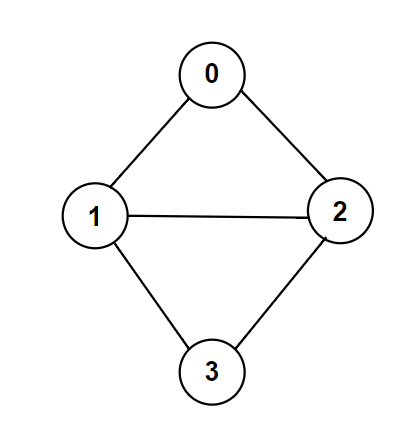
위 그래프에는 4개의 노드(0,1,2,3)와 5개의 간선이 있으며, 간선은 (0,1), (0,2), (1,2), (1,3), (2,3)입니다.
0 1 2 3
--------------
0 | 0 1 1 0
1 | 1 0 1 1
2 | 1 1 0 1
3 | 0 1 1 0
위와같이 인접 리스트 (Adjacency Matrix)에서는 노드의 개수가 V이고, 간선의 개수가 E일때, 인접 행렬을 V x V 크기의 2차원 배열로 그래프를 나타낼 수 있습니다.
행과 열이 만나는 지점의 값이 1이면 해당 노드들 간에 간선이 존재한다는 것을 의미합니다.
예를 들어, map[0][1] = 1은 노드 0과 노드 1 사이에 간선이 있음을 나타냅니다.
0 -> 1, 2
1 -> 0, 2, 3
2 -> 0, 1, 3
3 -> 1, 2
위와 같이 인접 리스트 (Adjacency List)에서는 노드의 개수가 V이고, 간선의 개수가 E일 때, 인접 리스트는 각 노드에 연결된 다른 노드들을 리스트로 표현합니다.
Java에서의 그래프 표현

인접 행렬 구현
public class SimpleAdjacencyMatrixGraph {
public static void main(String[] args) {
int V = 4; // 노드의 개수
int[][] adjMatrix = new int[V][V];
// 간선 추가
adjMatrix[0][1] = 1;
adjMatrix[1][0] = 1;
adjMatrix[0][2] = 1;
adjMatrix[2][0] = 1;
adjMatrix[1][2] = 1;
adjMatrix[2][1] = 1;
adjMatrix[1][3] = 1;
adjMatrix[3][1] = 1;
adjMatrix[2][3] = 1;
adjMatrix[3][2] = 1;
// 행렬 출력
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
System.out.print(adjMatrix[i][j] + " ");
}
System.out.println();
}
}
}
실행 결과
0 1 1 0
1 0 1 1
1 1 0 1
0 1 1 0
인접 리스트 구현
import java.util.LinkedList;
public class SimpleAdjacencyListGraph {
public static void main(String[] args) {
int V = 4; // 노드의 개수
LinkedList<Integer>[] adjList = new LinkedList[V];
// 리스트 초기화
for (int i = 0; i < V; ++i) {
adjList[i] = new LinkedList<>();
}
// 간선 추가
adjList[0].add(1);
adjList[1].add(0);
adjList[0].add(2);
adjList[2].add(0);
adjList[1].add(2);
adjList[2].add(1);
adjList[1].add(3);
adjList[3].add(1);
adjList[2].add(3);
adjList[3].add(2);
// 리스트 출력
for (int i = 0; i < V; ++i) {
System.out.print(i + " -> ");
for (Integer node : adjList[i]) {
System.out.print(node + " ");
}
System.out.println();
}
}
}
실행 결과
0 -> 1 2
1 -> 0 2 3
2 -> 0 1 3
3 -> 1 2'자료구조' 카테고리의 다른 글
| [Algorithm] 누적 합(Prefix Sum) 알고리즘 알아보기 (Java) (0) | 2024.07.18 |
|---|---|
| [JAVA] Deque (데크, 덱) 자료구조 알아보기 (0) | 2024.07.14 |
| [JAVA] HashSet 클래스 사용법 (중복 없는 데이터 집합) (0) | 2024.06.29 |
| [JAVA] HashMap_entrySet() : 데이터 접근과 반복을 간편하게 하는 방법(2/2) (0) | 2024.06.28 |
| [자료구조 JAVA] 우선순위 큐(Priority Queue) 클래스 알아보기 ✔ (0) | 2024.06.16 |
