
개요
알고리즘 풀이를 하다 보면 소수를 구할 때가 많습니다. 이때, 소수를 구하는 방식은 여러 가지가 있으며, 각각의 방식에 따라 시간 복잡도가 다르게 나타납니다.
가장 기본적인 방법은 O(N)의 시간 복잡도를 가진 소수 판별 함수를 사용하는 것입니다.
이 외에도 제곱근을 활용한 최적화 방법, 그리고 에라토스테네스의 체를 이용한 효율적인 소수 구하는 방법이 있습니다. 본 글에서는 이 세 가지 방법을 차례대로 살펴보겠습니다.
소수(Prime Number)란❓
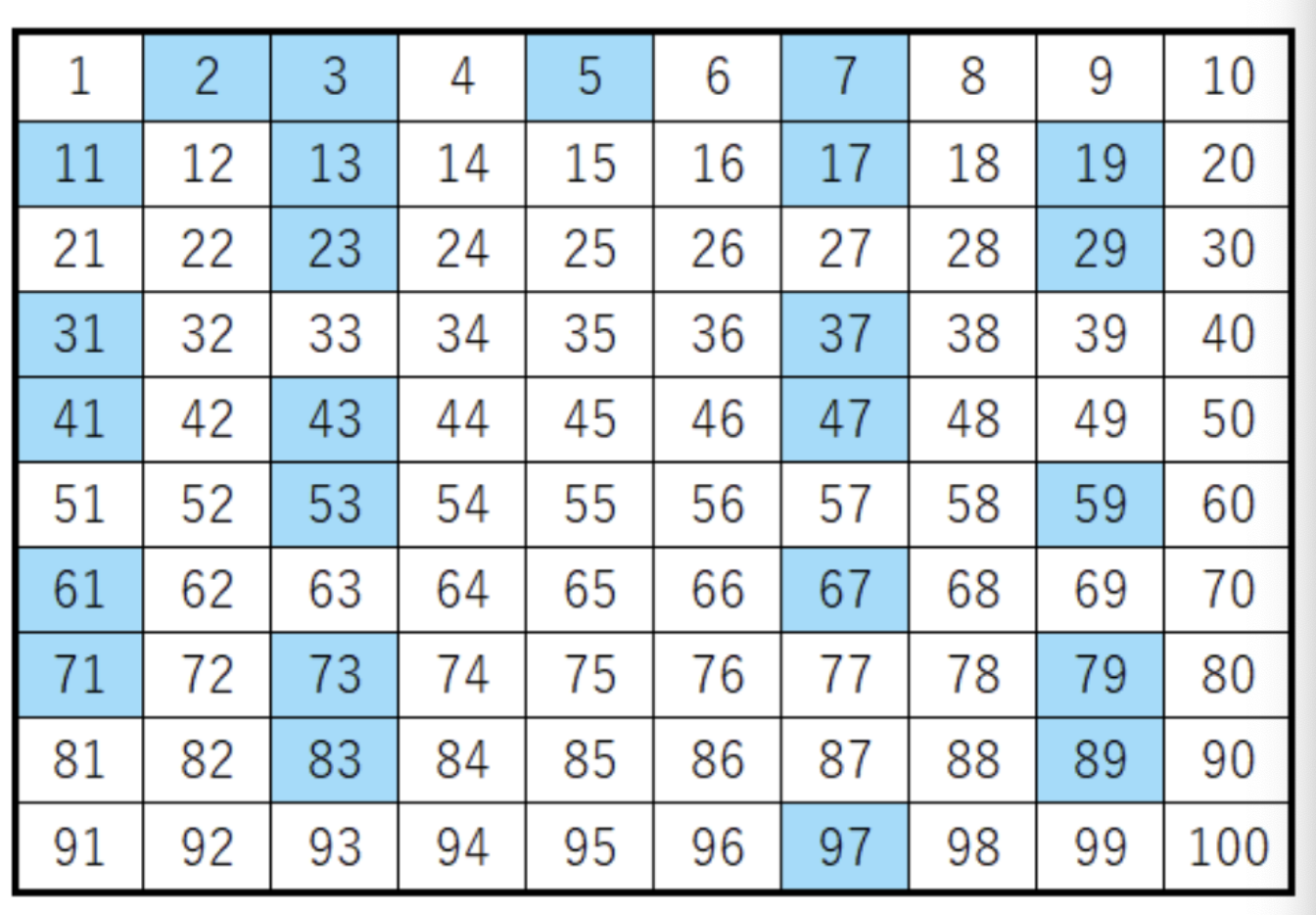
먼저 소수란 1과 자기 자신으로만 나누어 떨어지는 수로 "양의 약수를 두 개만 가지는 자연수"를 의미하며, 2, 3, 5, 7, 11 ... 등이 존재합니다.
기본 소수 판별 함수 (O(N))
가장 간단한 방법은 주어진 숫자에 대해 1부터 그 숫자까지의 모든 수로 나눠보는 방법입니다. 이 방식은 가장 직관적이고, 구현이 간단하지만 시간 복잡도가 O(N)입니다.
public static boolean isPrime(int n) {
if (n < 2) return false; // 2보다 작은 수는 소수가 아님
for (int i = 2; i < n; i++) {
if (n % i == 0) { // 나눠지면 소수가 아님
return false;
}
}
return true;
}
이 방식은 숫자 n에 대해 1부터 n-1까지 모두 나눠봐야 하기 때문에, 최악의 경우 O(N)의 시간이 걸립니다. 이 방법은 작은 범위에서는 문제가 되지 않지만, 큰 수에 대해서는 매우 비효율적입니다.
제곱근을 활용한 소수 판별 (O(√N))
기본 소수 판별은 모든 경우의 수를 나눠야 하기 때문에 매우 비효율적입니다. 실은 제곱근을 사용하면 보다 효율적으로 계산할 수 있습니다.
왜냐하면 8의 경우 약수는 (1,2,4,8)이 존재합니다. 이 때 1과 8을 제외하고, 2와 4는 2 * 4 = 4 * 2와 같이 서로 대칭을 이루기 때문입니다.
public static boolean isPrime(int n) {
if (n < 2) return false; // 2보다 작은 수는 소수가 아님
for (int i = 2; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
return false; // 나누어지면 소수가 아님
}
}
return true;
}
이 방식은 숫자 n의 제곱근까지 나눠보므로, 시간 복잡도는 O(√N)입니다. 이 방법은 기본적인 방법보다 훨씬 효율적이며, 큰 수에 대해서도 상대적으로 빠르게 동작합니다.
에라토스테네스의 체 (Sieve of Eratosthenes) 알고리즘
에라토스테네스의 체는 고대 그리스의 수학자 에라토스테네스(Eratosthenes)가 고안한, 소수를 효율적으로 구하는 알고리즘입니다.
주어진 범위 내에서 소수를 빠르게 찾는 방법으로, 숫자들의 배수를 제거하는 방식으로 소수를 구하는 원리입니다.
이 알고리즘은 소수를 구하는 데 있어 매우 효율적이며, 그 시간 복잡도는 O(n log n)입니다. 따라서 특정 범위 내에서 대량의 소수를 한꺼번에 판별하고자 할 때 사용합니다.
에라토스테네스의 체 (Sieve of Eratosthenes) 알고리즘의 동작원리
- 주어진 수의 범위에서 2부터 시작하여 숫자를 하나씩 체크합니다.
- 해당 숫자가 소수라면, 그 숫자의 배수를 모두 제외시킵니다.
- 숫자들이 모두 처리될 때까지 위 과정을 반복합니다.
- 남은 숫자들 중에서 배수로 제거되지 않은 숫자들이 소수입니다.
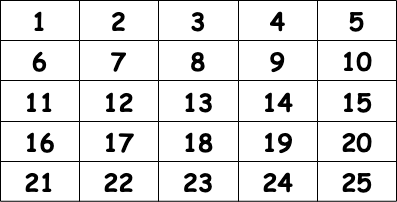
1. 2차원 배열 생성 후 값 초기화
2. 2부터 시작하여 배수를 모두 삭제
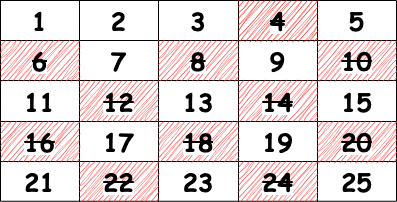
1은 소수가 아니기 떄문에 2부터 시작하여 특정 숫자에 배수에 해당하는 모든 숫자를 삭제합니다. 이 때 자기 자신의 숫자는 삭제하지 않습니다.
2. index = 3 : 3의 배수를 모두 삭제
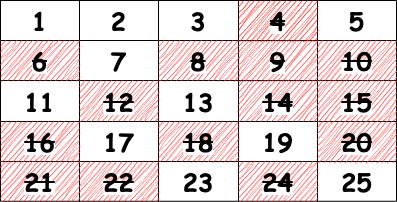
3일 때도 마찬가지로 자기 자신을 제외 한 배수의 모든 숫자를 삭제합니다. 이 때 이미 삭제된 숫자의 경우 건너 뜁니다. 3에서는 6,12,18, 24가 이미 삭제되었으므로 건너 뛰게 됩니다.
3. index = 4 : 4의 배수를 모두 삭제
- 4의 경우 이미 지워져 있기 때문에 건너 뜁니다.
4. inde = 4: 5의 배수를 모두 삭제
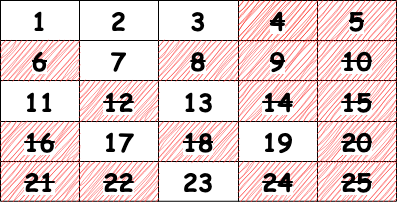
5도 마찬가지로 배수를 지워주면, 이후에는 삭제할 숫자가 없기 때문에 남아있는 숫자들을 출력합니다.
에라토스테네스의 체 (Sieve of Eratosthenes) 알고리즘 Java
public static boolean[] eratosthenes(int limit) {
// 0과 1은 소수가 아니므로 false로 초기화
boolean[] isPrime = new boolean[limit + 1];
Arrays.fill(isPrime, true); // 모든 수를 일단 소수로 가정
isPrime[0] = isPrime[1] = false; // 0과 1은 소수가 아니므로 false로 설정
// 2부터 limit까지 체크
for (int i = 2; i <= Math.sqrt(limit); i++) {
if (isPrime[i]) { // i가 소수일 경우
// i의 배수는 모두 소수가 아니므로 false로 설정
for (int j = i * i; j <= limit; j += i) {
isPrime[j] = false;
}
}
}
return isPrime;
}
public static void main(String[] args)throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine()); // 소수인지 판별할 숫자 input
eratosthenes(N);
}- boolean 배열의 default값은 false이기 때문에 fill()메서드로 true를 채워줍니다.
시간 복잡도: O(N log log N)
- 에라토스테네스의 체는 숫자 n에 대해 모든 배수를 제거하면서 소수를 구합니다.
- 이 알고리즘의 시간 복잡도는 O(N log N)으로, 매우 효율적이며 큰 범위에서도 빠르게 소수를 구할 수 있습니다.
'Algorithm' 카테고리의 다른 글
| [Algorithm] 파스칼의 삼각형 알고리즘 구현하기 (Java) (1) | 2024.12.03 |
|---|---|
| [Algorithm] 백트래킹(Backtracking) 알고리즘 알아보기 (0) | 2024.11.27 |
| [Algorithm] KMP(Knuth-Morris-Pratt) 알고리즘이란 무엇일까❓ (문자열 비교) (2) | 2024.11.14 |
| [Algorithm] 이진 탐색 알고리즘 : 데이터 정렬과 검색 최적화 (Binary Search, Java) (0) | 2024.07.09 |
| [Algorithm] 효율적인 그래프 탐색: 자바로 구현한 DFS 알아보기 (1/2) (0) | 2024.07.07 |