
문제설명

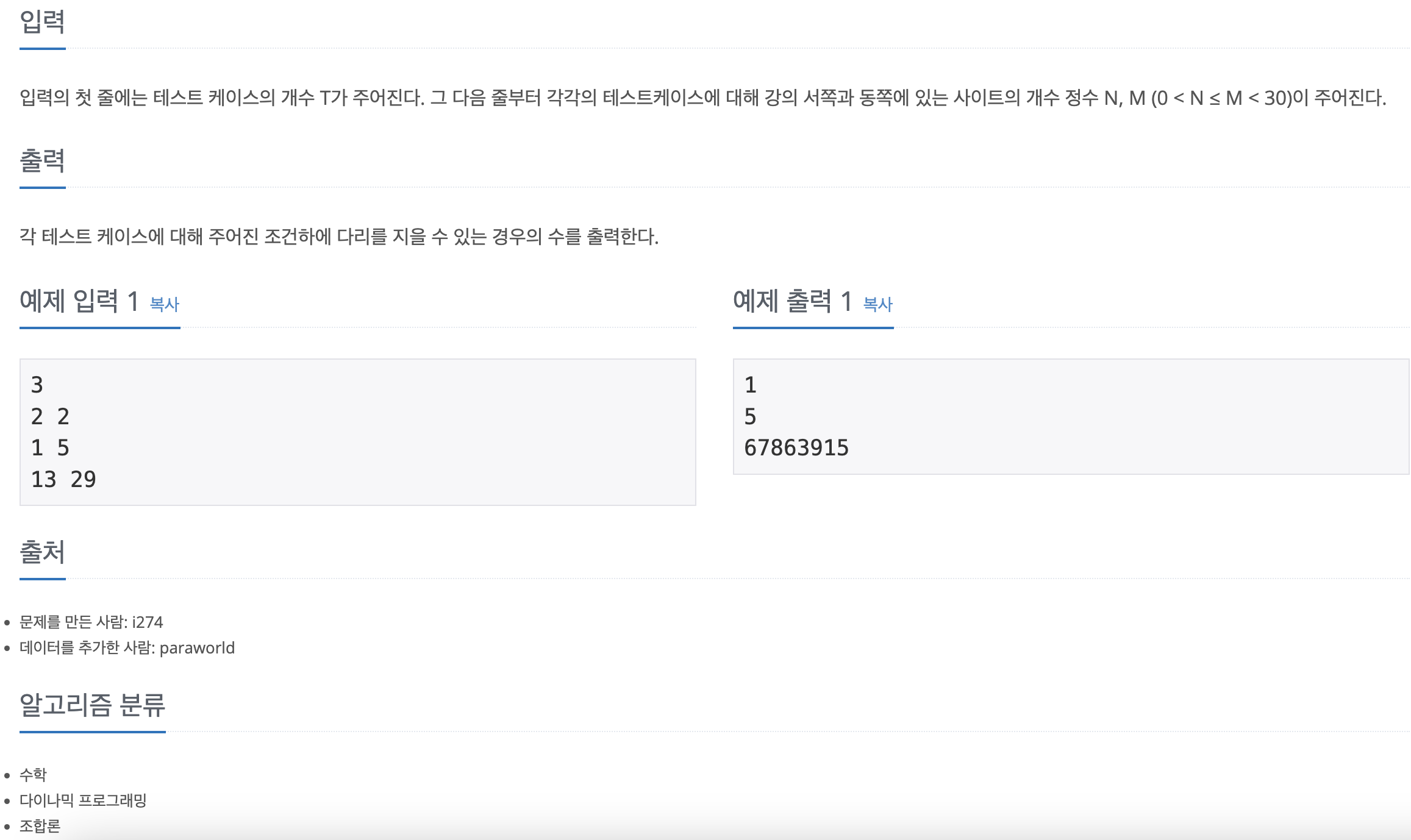
입력 & 출력
문제 이해하기
이번 "백준 - 다리 놓기"문제는 조합론을 활용하여 해결할 수 있는 문제입니다. 문제 자체는 어렵지 않으나 이항 계수의 공식이나 개념을 모른다면 쉽지 않은 문제입니다.
이 문제는 주어진 두 개의 사이트에서 최대한 많은 다리를 놓을 수 있는 방법을 구하는 문제로, 이항계수를 기반으로 풀 수 있습니다.
이항계수 : "n개 중에서 k개를 고르는 경우의 수"를 나타내며, 조합이라고도 불립니다.
문제를 해결하는 방법은 크게 두 가지로 나눌 수 있습니다.
- 첫 번째 : 이항계수를 직접 계산하는 방법으로, 팩토리얼을 활용하여 조합을 계산하는 방식입니다.
[백준, 11050번] 이항 계수 1 (수학, 구현, 조합론, Java)
문제설명입력 & 출력나의 풀이이번 문제는 "이항 계수 1" 문제로, 주어진 정수 n과 k를 입력받아 이항 계수를 계산하는 문제입니다.이항 계수란?이항 계수(Binomial Coefficient): 조합(combination)에서
pixx.tistory.com
- 두 번째 방법 : 동적 계획법(DP)을 활용하여 이전에 계산된 값을 저장하고 이를 이용해 효율적으로 조합을 구하는 방식입니다.
[Algorithm] 동적 계획법(Dynamic Programming, DP, Java) 알아보기
동적 계획법 DP란❓ 동적 계획법은 프로그래밍 대회 문제에 가장 자주 출현하는 디자인 패러다임 중 하나로 1940년대 리처드 벨만이 사용하던 용어입니다. 주로 줄여서 DP라고 많이 말하며, 주
pixx.tistory.com
먼저 문제 이해를 다시 해보겠습니다.
- 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다.
- 서쪽 사이트와 동쪽 사이트를 다리로 연결하려고한다, 이 때 한 사이트에는 한 개의 다리만 연결할 수 있다.
다리는 서로 겹칠 수 없다.
위 요구사항을 기반으로 그림으로 표현한다면 다음과 같습니다.

재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 합니다. N ≤ M이라고 했으니, 동쪽의 M개 사이트 중에서 N개를 선택해서 서쪽의 사이트들과 연결해야 합니다. 따라서 이는 M개 중 N개를 선택하는 조합 문제로 해결할 수 있습니다.
따라서 M개의 포인트 중에서 N개를 선택하는 경우의 수는 M choose N (mCn)으로 나타낼 수 있습니다

예를 들어, 서쪽에 2개, 동쪽에 4개의 사이트가 있는 경우의 모든 가능한 다리 배치의 경우의 수는 위와과 같습니다. (4C2)

위와 같은 이항 계수의 공식을 사용하여 4C2를 구해보자면,
- 공식으로는 4C2 = 4! / (2! × (4-2)!)입니다.
- 즉, 4! / (2! × 2!)
- 하나씩 계산해보면:
- 4! = 4 × 3 × 2 × 1 = 24
- 2! = 2 × 1 = 2
- 분모는 2! × 2! = 2 × 2 = 4
- 따라서:
- 4C2 = 24 / 4 = 6
이제, 이항 계수를 기반으로 2가지 풀이를 통해 답을 도출할 수 있습니다.
나의 풀이
1. 이항 계수 직접 계산 (팩토리얼 사용)

먼저 조합을 직접 팩토리얼로 계산하는 방법입니다. 이 때 문제에서 M이 최대 30까지 가능하기 때문에, 30!과 같은 매우 큰 수가 계산될 수 있습니다.
이런 큰 수는 int나 long으로는 감당할 수 없어 오버플로우가 발생할 수 있습니다. 그래서 제한 없이 큰 정수를 다룰 수 있는 BigInteger 클래스를 사용했습니다.
[JAVA] 큰 수 다루기 (BigInteger, BigDecimal)
보통 Java에서 정수형을 표현할 때 int형이나 큰 수일경우 long형을 사용합니다. 물론 byte와 short 도 있지만 잘 사용을 하지 않습니다.타입 할당되는 메모리의 크기 표현 범위byte1 byte- 128 ~ 127short 2 by
pixx.tistory.com
직접 팩토리얼을 계산하기 위해 getFactorialNumber() 함수를 만들고, 팩토리얼을 구해줍니다. 이 때 Biginteger에서 곱셈, 나눗셈은 일반적으로 사용되는 "*" , "/" 를 사용할 수 없고, Biginteger클래스의 multifly()와 devide()메서드를 사용해줘야 합니다.
2. 동적 계획법 DP 사용

다이나믹 프로그래밍(DP)를 사용하기 위해선 점화식이 중요합니다. 먼저 위와 같은 점화식이 나온이유는 다음과 같습니다.
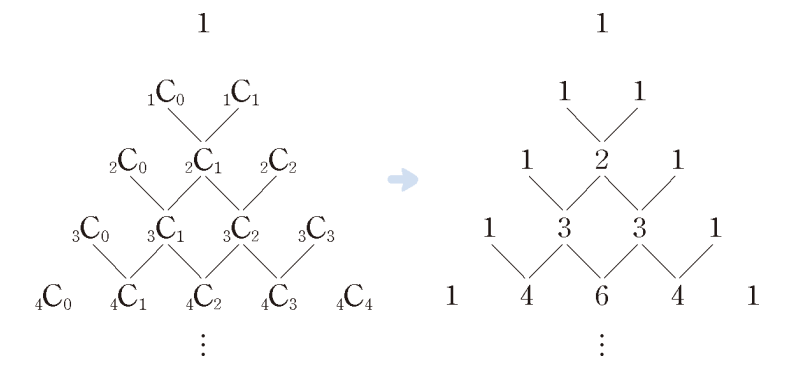
위 파스칼의 삼각형을 본다면 쉽게 점화식을 구할 수 있습니다.
- 각 행의 첫번째 값과 마지막 값은 항상 1입니다.
- 나머지 항목은 위쪽 두 개의 항목을 더한 값입니다.
즉, 다음 점화식을 따릅니다: C ( n , k ) = C ( n − 1 , k − 1 ) + C ( n − 1 , k )
따라서 위 두가지 경우를 사용하여 메모이제이션(Memoization)을 이용하면 해결할 수 있습니다.
문제에서 N과M은 30보다 크거나 작기 때문에 30의 크기를 가지는 dp배열을 전역변수로 선언해주고, 각 행의 첫번째와 마지막 값은 항상 1이기 때문에 초기값을 설정해줍니다.
그리고 점화식을 기준으로 배열을 채워주고 n과 m에 해당 하는 값을 리턴하여 마무리해주면 됩니다.

- 87091467 (다이나믹 프로그래밍 : DP)
- 87088977 (팩토리얼 직접 계산)
다이나믹 프로그래밍을 사용하여 풀이한 코드가 좀 더 메모리가 빠른 것을 확인 할 수 있습니다. 이는 메모이제이션으로 중복 계산을 피하고, 이전 계산 결과를 재사용하여 효율적이기 때문입니다.
'Coding Test > 백준' 카테고리의 다른 글
| [백준, 15650] N과 M (2) (백트래킹, Java) (0) | 2024.12.12 |
|---|---|
| [백준, 2579번] 계단 오르기 (다이나믹 프로그래밍 : DP, Java) (0) | 2024.12.12 |
| [백준, 11866번] 요세푸스 문제 0 (구현, 큐 Queue , Java) (1) | 2024.12.01 |
| [백준, 1018번] 체스판 다시 칠하기 (브루트 포스, Java) (0) | 2024.11.30 |
| [백준, 1463번] 1로 만들기 (동적 계획법DP, Java) (0) | 2024.11.28 |
