문제설명

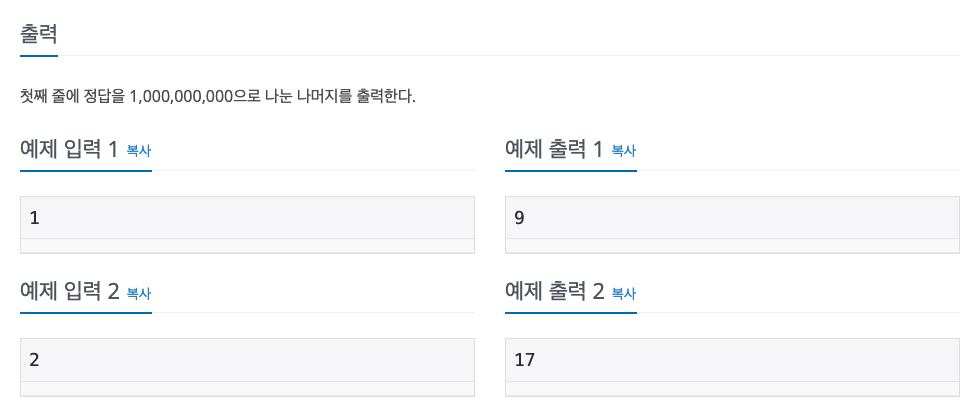
입력 & 출력
나의 풀이
문제 접근 방법
"백준 - 쉬운 계단 수" 문제는 계단수의 개수를 구하는 문제입니다.
[TIL, 일일 회고] 2025.01.02 - 계단 수란? (DP, 재귀)
백준 - 쉬운 계단 수" 문제를 풀다가 계단 수의 대한 개념이 나와 정리하고자합니다. 계단 수 란❓계단수는 수학에서 전통적인 개념은 아니지만, 알고리즘 문제에서 주로 등장하는 특수한 형태
pixx.tistory.com
위 포스팅에서 정리했듯이 계단수는 수학적으로 일반적으로 다루는 개념은 아니어서 생소할 수 있습니다. 하지만 문제에서 설명하듯이, 계단수란 각 자리 숫자 간의 차이가 1인 수를 의미합니다. 예를 들어, 45656은 인접한 모든 자리의 차이가 1인 계단수입니다.
N 길이가 주어질 때 각 계단수를 살펴보면 다음과 같습니다.
1자리 수
- 개수: 9개
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
2자리 수
- 개수: 17개
- 10, 12, 21, 23, 32, 34, 43, 45, 54, 56, 65, 67, 76, 78, 87, 89, 98
3자리 수
- 개수: 32개
- 101, 121, 123, 210, 212, 232, 234, 321, 323, 343, 345, 432, 434, 454, 456, 543, 545, 565, 567, 654, 656, 676, 678, 765, 767, 787, 789, 876, 878, 898, 987, 989
1자리 수를 보면 1부터 9까지 존재하고, 2자리 수를 보면 1자리 수에서 1을 더하거나 뺀 수인 것을 알 수 있습니다.
다시 문제를 살펴보면, 계단수는 인접한 모든 자리의 차이가 1이어야 합니다. 즉, 각 자릿수에서 바로 이전 자리와의 차이가 ±1이어야 합니다.
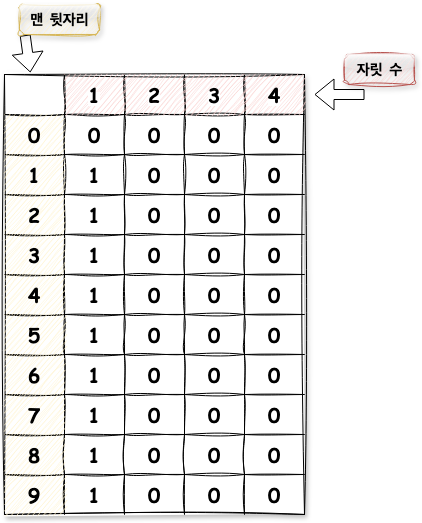
위 그림을 보면 1자리 수는 [1, 2, 3, 4, 5, 6, 7, 8, 9]로 1개만 존재합니다. 이를 기반으로 2자리 수를 생각해보겠습니다.
- 1️⃣ → 맨앞이
0이 올 수는 없기 때문에 맨 뒷자리가 1이 올 수 있는 2자리의 수는 "21" 즉, 1개만 존재합니다. - 2️⃣ → 맨 뒤가 2가 오는 2자리의 계단 수는 앞자리가 1 또는 3이어야 하기 때문에 "12", "32" 즉, 2개가 존재합니다.
- 3️⃣ → 맨 뒤가 3이 오는 2자리의 계단 수는 앞자리가 2 또는 4이어야 하기 때문에 "23", "43" 즉, 2개가 존재합니다.
- ..9️⃣ → 맨 뒤가 9가 오는 2자리의 계단 수는 앞자리가 8밖에 없습니다. "89" 즉, 1개만 존재합니다.
위 과정을 통해 계단 수의 특징을 알 수 있습니다. 각 자릿수에서 맨 뒷자리가 일 때, 그 앞자리는 또는 이 와야 한다는 규칙을 알 수 있습니다. 이를 기반으로 점화식을 도출할 수 있습니다.
계단 수를 구하는 데 있어 핵심은, 현재 자릿수의 맨 뒷자리 가 될 수 있는 수는 이전 자릿수에서 j−1j-1과 j+1j+1이었을 때만 가능하다는 것입니다. 이를 점화식으로 나타내면:
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1]
(단, j−1과 이 0 이상, 9 이하의 범위일 때만 적용됩니다.)
즉, i자리의 수에서 맨 뒤가 j일 때, 이전 자리가 또는 일 수 있으므로, 이를 더한 값이 현재 자리에 올 수 있는 계단 수가 됩니다.
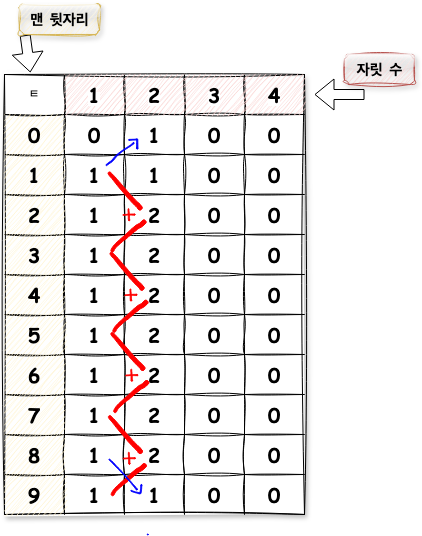
0과 9인 경우만 제외하고, 점화식을 토대로 값을 채워나가면 위와 같이 형성되게 됩니다. 이 때 0과 9는 경계값이기 때문에, 0일 경우는 앞자리가 1만 올 수 있고, 9일 경우는 앞자리가 8만 올 수 있다는 특수한 규칙이 적용됩니다.
이런식으로 DP 배열의 값을 재사용하면서 채워나가면 다음과 같은 배열이 형성됩니다.

전체 코드
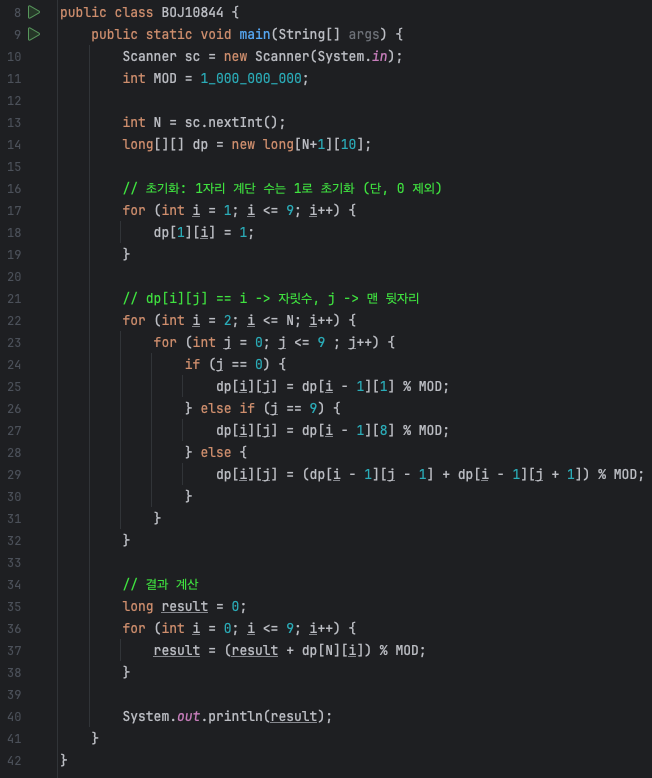
점화식을 사용하여 DP 배열을 생성한 후, 각 i번째 자리수의 계단 수를 더하여 최종 자리수에 해당하는 계단 수의 총합을 구합니다. 그 후, 구한 값을 1,000,000,000으로 나눈 나머지를 출력하면 최종 답을 얻을 수 있습니다.
문제의 핵심은 점화식을 생성하는 것이고, 주의해야할 점은 0과 9는 특수한 규칙을 적용해야한다는 것입니다.
'Coding Test > 백준' 카테고리의 다른 글
| [백준, 14501번] 퇴사 (다이나믹 프로그래밍 : DP, Java) (0) | 2025.01.04 |
|---|---|
| [백준, 1927] 최소 힙 (우선순위 큐, Java) (1) | 2025.01.03 |
| [백준, 2156번] 포도주 시식 (다이나믹 프로그래밍 : DP, 동적 계획법 , Java) (2) | 2025.01.01 |
| [백준, 1654번] 랜선 자르기 (이진 탐색, 이분 탐색, Java) (0) | 2024.12.31 |
| [백준, 2805번] 나무 자르기 (이진 탐색, 이분 탐색, Java) (0) | 2024.12.30 |

